您当前位置：首页 > php开源 > 综合技术 > Codeforces Round #389 (Div. 2) C. Santa Claus and Robot 贪心+最短路

Codeforces Round #389 (Div. 2) C. Santa Claus and Robot 贪心+最短路

来源：程序员人生发布时间：2017-02-07 09:10:57 阅读次数：2731次

Santa Claus has Robot which lives on the infinite grid and can move along its lines. He can also, having a sequence of m pointsp1, p2, ..., pm with integer coordinates, do the following: denote its initial location by p0. First, the robot will move from p0 to p1 along one of the shortest paths between them (please notice that since the robot moves only along the grid lines, there can be several shortest paths). Then, after it reaches p1, it'll move to p2, again, choosing one of the shortest ways, then to p3, and so on, until he has visited all points in the given order. Some of the points in the sequence may coincide, in that case Robot will visit that point several times according to the sequence order.

While Santa was away, someone gave a sequence of points to Robot. This sequence is now lost, but Robot saved the protocol of its unit movements. Please, find the minimum possible length of the sequence.

Input

The first line of input contains the only positive integer n (1 ≤ n ≤ 2·105) which equals the number of unit segments the robot traveled. The second line contains the movements protocol, which consists of n letters, each being equal either L, or R, or U, or D. k-th letter stands for the direction which Robot traveled the k-th unit segment in: L means that it moved to the left, R — to the right, U — to the top and D — to the bottom. Have a look at the illustrations for better explanation.

Output

The only line of input should contain the minimum possible length of the sequence.

Examples

input
4
RURD

output
2

input
6
RRULDD

output
2

input
26
RRRULURURUULULLLDLDDRDRDLD

output
7

input
3
RLL

output
2

input
4
LRLR

output
4

Note

The illustrations to the first three tests are given below.

$\text{[math]}$ $\text{[math]}$ $\text{[math]}$

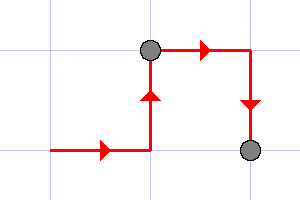
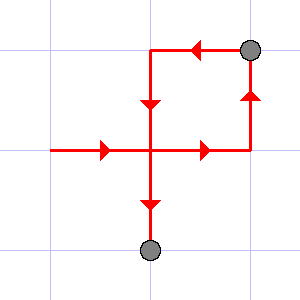
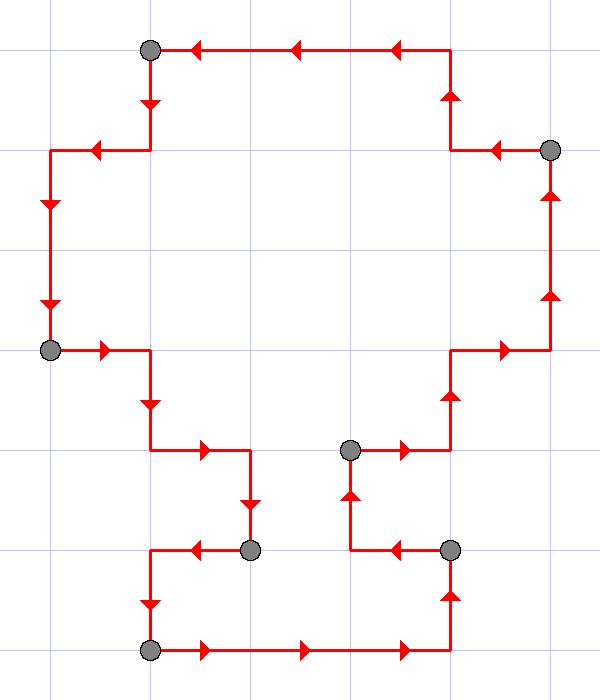
The last example illustrates that each point in the sequence should be counted as many times as it is presented in the sequence.

Source

Codeforces Round #389 (Div. 2, Rated, Based on Technocup 2017 - Elimination Round 3)

My Solution

题意：给定1个路径，让找出尽量少的关键点，没相邻的2个关键点的路径必须是最短路径

贪心+最短路

这是1个很有趣的题 Y ^_^ Y

ans = 0;

(px,py)表示最近出现的1个关键点坐标，cnt表示从最近的那个关键点到当前点所走的路程， (x, y)表示当前所在的点的坐标。

然后每步更新cnt及(x, y)后判断abs(px - x) + abs(py - y) == cnt，如果成立则从最近的1个关键点到当前点1直在根据最短路走，直到每次出现不公道的情况，则上1个点更新为新的最近的关键点，并且ans++，扫1遍，最后1个点必定是关键点，故额外 ans++ 把最后1个点加上。

复杂度 O(n)

#include <iostream>
#include <cstdio>
#include <string>
#include <cmath>
using namespace std;
typedef long long LL;
const int maxn = 1e6 + 8;

string s;

int main()
{
    #ifdef LOCAL
    freopen("c.txt", "r", stdin);
    //freopen("c.out", "w", stdout);
    int T = 8;
    while(T--){
    #endif // LOCAL
    ios::sync_with_stdio(false); cin.tie(0);

    int n, px = 0, py = 0, x = 0, y = 0, rx = 0, ry = 0, ans = 0, cnt = 0;
    cin >> n;
    cin >> s;
    bool flag = false;
    for(int i = 0; i < n; i++){
        rx = x, ry = y;

        if(s[i] == 'L'){
            x--;
        }
        else if(s[i] == 'R'){
            x++;
        }
        else if(s[i] == 'U'){
            y++;
        }
        else if(s[i] == 'D'){
            y--;
        }

        cnt++;
        if(abs(px - x) + abs(py - y) == cnt){
            //if(!flag){ans++; flag = true; }
        }
        else{
            ans++;
            //if(flag) ans++;

            cnt = 1;
            px = rx;
            py = ry;
            //cout << px << ' ' << py << endl;

        }
    }
    ans++;
    cout << ans << endl;



    #ifdef LOCAL
    cout << endl;
    }
    #endif // LOCAL
    return 0;
}

Thank you!

------from ProLights

生活不易，码农辛苦
如果您觉得本网站对您的学习有所帮助,可以手机扫描二维码进行捐赠
程序员人生

------分隔线----------------------------

上一篇 MySQL索引原理及慢查询优化

下一篇 HDU 1556 Color the ball【线段树区间更新，一次查询+数组模拟】

分享到:

------分隔线----------------------------

會飛的魚

积分：65

3粉丝

0关注

栏目热点