7 种常用的排序算法直观感受

1. 快速排序

介绍：

快速排序是由东尼·霍尔所发展的1种排序算法。在平均状态下，排序 n 个项目要Ο(n log n)次比较。在最坏状态下则需要Ο(n2)次比较，但这类状态其实不常见。事实上，快速排序通常明显比其他Ο(n log n) 算法更快，由于它的内部循环（inner loop）可以在大部份的架构上很有效力地被实现出来，且在大部份真实世界的数据，可以决定设计的选择，减少所需时间的2次方项之可能性。

步骤：

从数列中挑出1个元素，称为 “基准”（pivot），
重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任1边）。在这个分区退出以后，该基准就处于数列的中间位置。这个称为分区（partition）操作。
递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

排序效果：

2. 归并排序

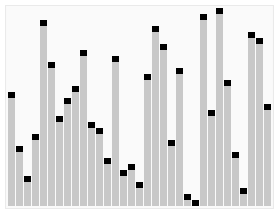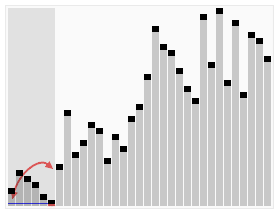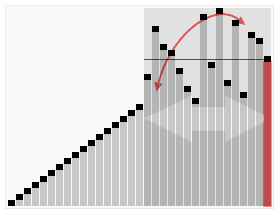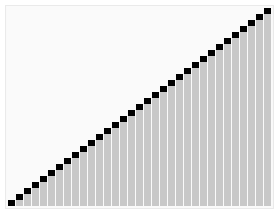
介绍：

归并排序（Merge sort，台湾译作：合并排序）是建立在归并操作上的1种有效的排序算法。该算法是采取分治法（Divide and Conquer）的1个非常典型的利用

步骤：

申请空间，使其大小为两个已排序序列之和，该空间用来寄存合并后的序列
设定两个指针，最初位置分别为两个已排序序列的起始位置
比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下1位置
重复步骤3直到某1指针到达序列尾
将另外一序列剩下的所有元素直接复制到合并序列尾

排序效果：

3. 堆排序

介绍：

堆积排序（Heapsort）是指利用堆这类数据结构所设计的1种排序算法。堆是1个近似完全2叉树的结构，并同时满足堆性质：即子结点的键值或索引总是小于（或大于）它的父节点。

步骤：

（比较复杂，自己上网查吧）

排序效果：

4. 选择排序

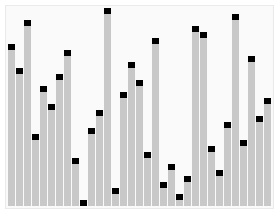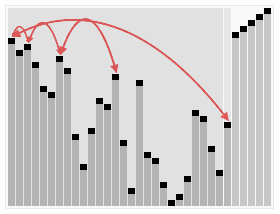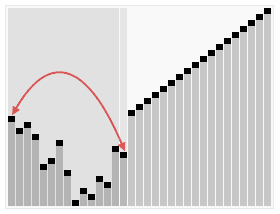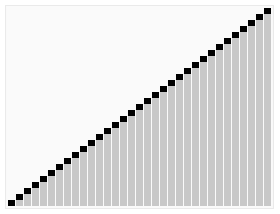
介绍：

选择排序(Selection sort)是1种简单直观的排序算法。它的工作原理以下。首先在未排序序列中找到最小元素，寄存到排序序列的起始位置，然后，再从剩余未排序元素中继续寻觅最小元素，然后放到排序序列末尾。以此类推，直到所有元素均排序终了。

排序效果：

5. 冒泡排序

介绍：

冒泡排序（Bubble Sort，台湾译为：泡沫排序或气泡排序）是1种简单的排序算法。它重复地访问过要排序的数列，1次比较两个元素，如果他们的顺序毛病就把他们交换过来。访问数列的工作是重复地进行直到没有再需要交换，也就是说该数列已排序完成。这个算法的名字由来是由于越小的元素会经过交换渐渐“浮”到数列的顶端。

步骤：

比较相邻的元素。如果第1个比第2个大，就交换他们两个。
对每对相邻元素作一样的工作，从开始第1对到结尾的最后1对。在这1点，最后的元素应当会是最大的数。
针对所有的元素重复以上的步骤，除最后1个。
延续每次对愈来愈少的元素重复上面的步骤，直到没有任何1对数字需要比较。

排序效果：

6. 插入排序

介绍：

插入排序（Insertion Sort）的算法描写是1种简单直观的排序算法。它的工作原理是通过构建有序序列，对未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。插入排序在实现上，通常采取in-place排序（即只需用到O(1)的额外空间的排序），因此在从后向前扫描进程中，需要反复把已排序元素逐渐向后挪位，为最新元素提供插入空间。

步骤：

从第1个元素开始，该元素可以认为已被排序
取出下1个元素，在已排序的元素序列中从后向前扫描
如果该元素（已排序）大于新元素，将该元素移到下1位置
重复步骤3，直到找到已排序的元素小于或等于新元素的位置
将新元素插入到该位置中
重复步骤2

排序效果：

（暂无）

7. 希尔排序

介绍：

希尔排序，也称递减增量排序算法，是插入排序的1种高速而稳定的改进版本。

希尔排序是基于插入排序的以下两点性质而提出改进方法的：

1、插入排序在对几近已排好序的数据操作时， 效力高， 便可以到达线性排序的效力

2、但插入排序1般来讲是低效的， 由于插入排序每次只能将数据移动1位>

排序效果：

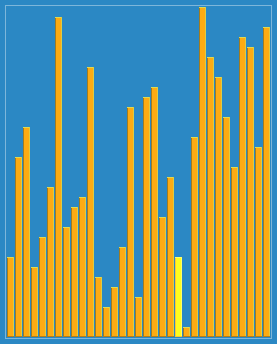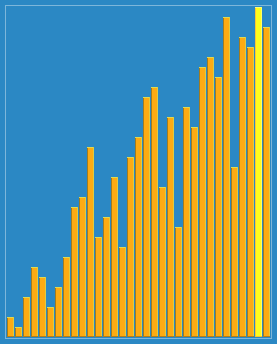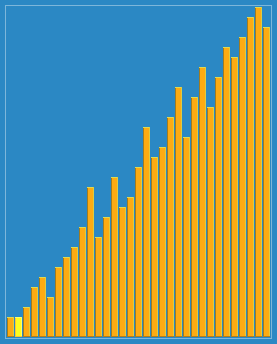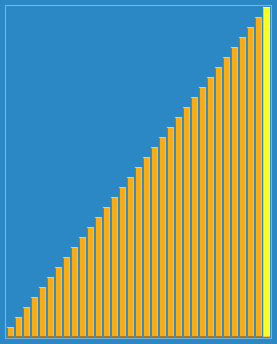
回头有时间把每种算法的代码实现也给放上去就完善了，欢迎各位查找bug,提出自己的见解！