第9章

• 前言
• 甚么是卷积
• 神经网络里卷积的目的
• 甚么是池化
• 卷积和池化的强先验

前言

卷积网络也叫卷积神经网络（或CNN），是1种特殊的深层的神经网络模型，它合适于时间序列数据的处理和图象数据处理。

这章内容主要讨论内容：

• 甚么是卷积
• 使用卷积的动机
• 甚么是池化
• 用于实践中的神经网络的几个变化卷积函数
• 卷积如何利用于各种维度不同的数据
• 讨论1些如何使卷积神经更有效力

补充内容：

卷积神经网络的特殊性体现在两个方面，1方面它的神经元间的连接是非全连接的， 另外一方面同1层中某些神经元之间的连接的权重同享的（即相同的）。它的非全连接和权值同享的网络结构使之更类似于生物神经网络，下降了网络模型的复杂度（对很难学习的深层结构来讲，这是非常重要的），减少了权值的数量。

9.1卷积运算

卷积运算是通过两个函数$f$和$g$ 生成第3个函数的1种数学算子，表征函数$f$与$g$经过翻转和平移的堆叠部份的面积。（百度百科）

为了说明卷积运算，我们1个通过激光传感器来定位飞船位置的例子。
$x(t)$：激光传感器的输出
$t$:某个时刻，这2个 变量都是实数

假定:激光传感器有1定的噪声，为了取得较小的噪声，我们采取了几种丈量方式，越新的测试方法，越可靠，所以我们给定比较新的丈量方法，更大的权重。我们得到权重函数：$w(a)$，变量$a$是丈量的年代。如果我们将这个函数利用到每个时刻，我们的得到了1个新的函数：
$s(t) = \int x(a)w(t − a)da$

这个操作叫卷积，通常卷积定义为：$s(t) = (x ∗ w)(t)$

$w$代表几率密度函数，或带有权重的均值。对卷积函数第1个函数$x$，被称作输入，第2个$w$，被称作核函数。如果激光传感器每秒丈量1次，$t$就是1个整数集合。$\displaystyle s(t) = (x ∗ w)(t) =\sum _{a=-\infty}^{\infty}x(a)w(t-a)$
我们常常会用卷积操作1个多坐标数据，比如我们用1个2维的图片作为输入，一样用2维的核$K$：

$\displaystyle S(i,j) = (I * K)(i,j) = \sum_m \sum_n I(m,n)K(i-m)(j-n)$

卷积的可计算性，我们可以等效的写成：
$\displaystyle S(i,j) = (K * I)(i,j) = \sum_m \sum_n I(i-m,j-n)K(m)(n)$

卷积运算的交换律的出现，是由于我们可以翻转核函数和输入值。很多深度学习库，都实现了相互关的函数。它和卷积是1样的，不过没有翻转核函数。
$\displaystyle S(i,j) = (I * K)(i,j) = \sum_m \sum_n I(i+m,j+n)K(m)(n)$
1个基于核翻转卷积算法将学习到相不翻转内核无需翻转由算法学到的内核。这也是很难看到单独使用卷积到机器学习;卷积1般和其他算法组合使用，这些组合函数不管使用翻转核卷积运算还是非翻转核卷积运算都不再变换。

图9.1：非核翻转2-D卷积的1个例子。在这类情况下，我们限制输出的位置，其中核数据完全位于图象内，在某些情况下，被称为有效卷积。我们用正方形上的箭头唆使左上角输入矩阵数据的元素通过施加右上角输入矩阵的区域的核数据，进行1个相互关计算。

9.2使用卷积的动机

卷积充分利用3个重要观点来改良深度学习系统：稀疏连接，参数同享和等效表示。另外，卷积提供了1种方法，来处理可变长的输入数据。传统的神经网络使用每个参数矩阵和输入矩阵相乘，算出输出值，这意味着每一个输出单元和输入单元都相互作用。卷积网络是稀疏连接的，这个是通过1个比输入小的核来实现的。比如，当处理图象时，这个输入图片，有成千或百万像素，但我们可以检测到1些小的有用的特点，比如核占据的几10或上百的像素的1些边沿。这意味着我们只需要保存更少的参数，这样可以下降模型所需内存，改良它的统计效力。如果存在1个m维的输入数据，和n维的输出数据，那末矩阵相乘需
要$m × n$个参数，算法需要1个$O(m × n)$复杂度。如果我们限制输出层的链接个数为$k$，那末仅仅需要$O(k × n)$复杂度。对稀疏连接的图片展现，可以参考图9.2和图9.3.在卷积神经网络里， 隐含层单元没必要直接和每个输入层神经单元互联，如图9.4。

图9.2：稀疏连接，从图片的下脸部分可知：我们高亮了输入单元$x3$,也高亮了受输入单元$x3$影响的输出单元，只有3个输出单元受它影响。（图底部）当$s$是由矩阵相乘得到，那末连接性不再是稀疏的，所有的输出单元都遭到它的影响。

图9.3

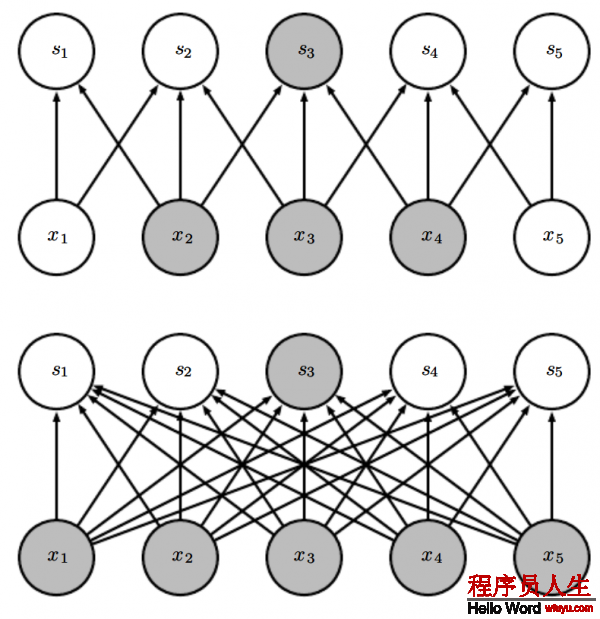
图9.4

图9.4：卷积神经网络里的深层神经单元的感知野比浅层神经元的感知野要大很多，如果神经网络里加入1些像步长卷积或池化，那末这个效果会增强。这意味着即便即便在在卷积神经网络里进行全连接,也会变得稀疏，在深层的神经元可以不和所有或大多数输入神经元连接。
参数同享是指在模型中的多个函数同享相同的参数。在传统的神经网络里，在计算输出层时候，权重矩阵的每个元素都会被计算1次，然后就不再使用。至于参数同享的代名词，也能够说，网络连接权重，由于既然权值可以利用到1个输入单元上，那末就能够利用到任何地方。在卷积神经网络，核中的每一个元素都被利用到输入数据的每一个元素中（除也许有些边界像素，这取决于边界的设计决策）。通过卷积运算使用的参数的同享意味着我们不是在每个位置上都学习1组独立的参数，而是我们只学1组参数。这不会影响前向反馈算法-它依然是$O(k × n)$存储空间，但是它进1步减少了模型的存储需求。回想当$k$通常是远远小于$m$几个数量级。
由于$m$和$n$通常大小大致相同，$k$与$M×N$相比是几近微不足道。卷积因此和密度矩阵乘法相比，在内存使用和统计效力方面更高效，为描写参数同享是如何工作的,参见图9.5.

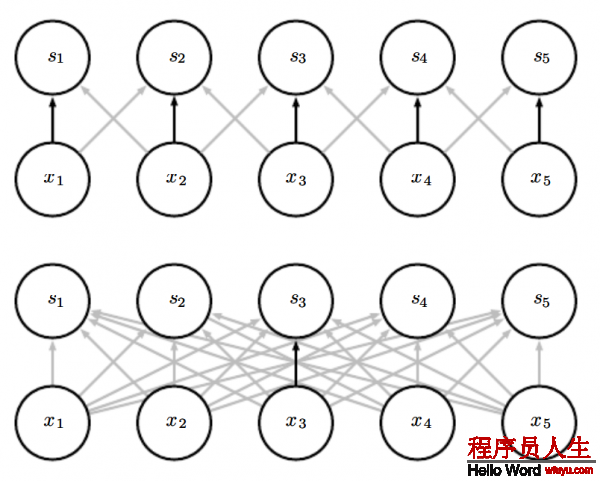
图 9.5:
权值同享:黑色箭头表示用某个特定的参数来连接2个不同模型。（上面）黑色箭头表示在卷积神经模型里我们使用3个核元素中的中间那个元素。由于权重同享这个参数被所有的输入单元使用。（下面）单个那个黑色箭头表明权值矩阵的中间那个元素在1个全连接的网络模型中被使用。这个模型里参数没有被同享只是被使用了1次。

作为1个实战中利用前2个原理（稀疏连接，参数同享）的1个实例，图9.6 表明了，稀疏连接，参数同享如何在图片中检测边的线性函数提高了效力。

在卷积时，由于权重同享而产生的1个特性叫转换等效性,如果说1个函数是等效的，那末意味着在输入中变化，那末在输出中也会一样变化。如果满足：f(g(x))=g 生活不易，码农辛苦
如果您觉得本网站对您的学习有所帮助,可以手机扫描二维码进行捐赠