Coursera机器学习-第六周-Advice for Applying Machine Learning

Evaluating a Learning Algorithm

---

Desciding What to Try Next
先来看1个有正则的线性回归例子：

当在预测时，有很大的误差，该如何处理？

1.得到更多的训练样本
2.选取少许的特点
3.得到更多的特点项
4.加入特点多项式
5.减少正则项系数$\lambda$
6.增加正则项系数$\lambda$

很多人，在遇到预测结果其实不理想的时候，会凭着感觉在上面的6个方案当选取1个进行，但是常常花费了大量时间却得不到改进。

因而引入了机器学习诊断，在后面会详细论述，

---

Evaluating a Hypothesis
怎样用你学过的算法来评估假定函数 ,讨论如何避免 过拟合和欠拟合的问题。
对这个简单的例子，我们可以对假定函数$h_\theta{(x)}$ 进行画图 ，然后视察图形趋势， 但对特点变量不止1个的这类1般情况 ，还有像有很多特点变量的问题 想要通过画出假定函数来进行视察，就会变得很难乃至是不可能实现。因此， 我们需要另外一种方法来评估我们的假定函数 。

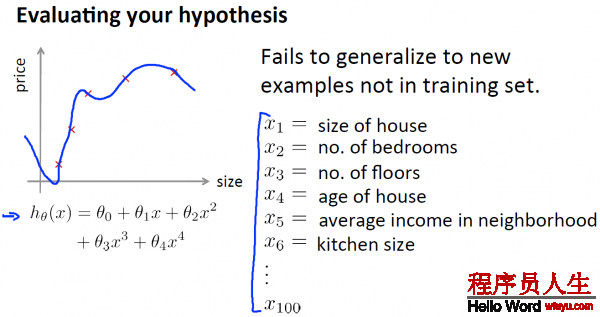
以下，给出了1种评估假定函数的标准方法：

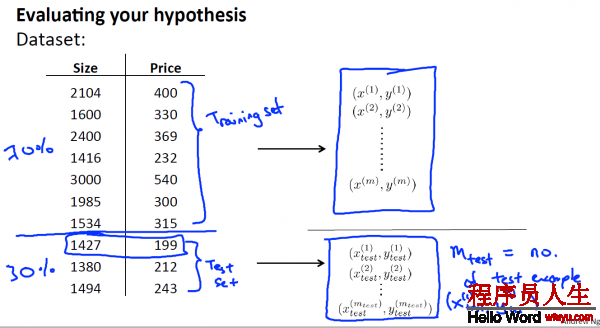
将这些数据集分为两个部份：Training set 和 Test set, 即是 训练集和测试集，
其中1种典型的分割方法是， 依照7:3的比例 ，将70%的数据作为训练集， 30%的数据作为测试集 。

PS：如果数据集是有顺序的话，那末最好还是随机取样。比如说上图的例子中，如果price或size是按递增或递减排列的话，那末就应当随机取样本，而不是将前70%作为训练集，后30%作为测试集了。

接下来 这里展现了1种典型的方法，你可以依照这些步骤训练和测试你的学习算法 比如线性回归算法 。首先 ，你需要对训练集进行学习得到参数$\theta$， 具体来说就是最小化训练误差$J{(\theta)}$ ，这里的$J{(\theta)}$ 是使用那70%数据 来定义得到的，也就是仅仅是训练数据 。接下来，你要计算出测试误差，用$J_{test}(\theta)$来表示测试误差, 那末你要做的就是 取出你之前从训练集(Training set)中学习得到的参数$\theta$放在这里, 来计算你的测试误差 $J_{test}{(\theta)}$

$J_{test}{(\theta)}$分为Linear Regreesion与Logistic Regression：

Linear Regreesion error:

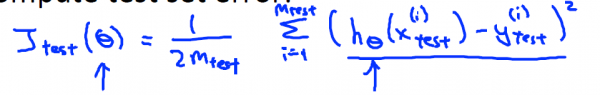
Logistic Regression error:

---

Model Selection and Train/Validation/Test sets

假设你想要肯定对某组数据， 最适合的多项式次数是几次 ？怎样选用正确的特点来构造学习算法 或假设你需要正确选择 学习算法中的正则化参数λ ，你应当怎样做呢？

Model Selection:

1.首先，建立d个model 假定（图中有10个，d表示其id），分别在training set 上求使其training error最小的θ向量，那末得到d个$\theta$

2.然后，对这d个model假定，带入$\theta$，在cross validation set上计算$J_{CV}$，即cv set error最小的1个model 作为 hypothesis，以下图中$|J_{(CV)}|$在第4组中最小，便取d=4的假定。

PS: 其实d表示dimension，也就是维度，表示该hypothesis的最大polynomial项是d维的。
PS’: 1般地，$|J_{(CV)}|$是大于等于$|J_{(train)}|$的,| * |表示数量

选择第1个模型($d=1$)， 然后求训练误差的最小值$J_{train}(\theta^{(1)})$ 这样你就会得到 1个参数向量$\theta^{(1)}$ 然后你再选择第2个模型($d=2$) 2次函数模型 ,进行一样的进程 这样你会得到另外一个参数向量 $\theta^{(2)}$，以此类推，直到第10个模型($d=10$),10次函数模型，训练误差最小值$J_{train}(\theta^{(10)})$。

接下来，我们需要做的是对所有这些模型，求出测试集误差(Test Error),顺次求出$J_{test}(\theta^{(1)})$~$J_{test}(\theta^{(10)})$当选取测试集误差最小的作为多项式模型。

这里选择的是5项式。那末问题来了，现在我想知道这个模型能不能很好地推行到新样本，我们还能通过测试集来验证1般性吗？这看起来仿佛有点不公道，由于我们刚才是通过测试集跟假定拟合来得到多项式次数$d$这个参数，也就是说我们选择了1个能够最好地拟合测试集的参数$d$的值，因此，我们的参数向量$\theta^{(5)}$在拟合测试集时的结果，极可能致使1个比实际泛化误差更完善的预测结果，也就是说泛化能力不足！

所以，为了解决这个问题，在模型选择中，我们将数据集不单单是分为训练集，测试集，而是分为训练集，交叉验证集和测试集{60%,20%,20%}的比例

1种典型的分割比例是 将60%的数据分给训练集，大约20%的数据给交叉验证集 ，最后20%给测试集。这个比例可以略微调剂，但这类分法是最典型的。

依照上面所述的步骤，这里不再赘述！ （详情在上面Model Selection下面有解释）

---

Bias vs. Variance

当你运行1个学习算法时 ，如果这个算法的表现不理想， 那末多半是出现 两种情况 ：要末是偏差比较大， 要末是方差比较大， 换句话说， 出现的情况要末是欠拟合， 要末是过拟合问题 。
那末这两种情况， 哪一个和偏差有关， 哪一个和方差有关， 或是否是和两个都有关 。弄清楚这1点非常重要 ，由于能判断出现的情况， 是这两种情况中的哪种， 实际上是1个很有效的唆使器， 指引着可以改进算法的 ，最有效的方法和途径 。

1. bias指hypothesis与正确的hypothesis(如果有的话)的偏差.
2. varience是指各样本与hypothesis的偏差和

---

Diagnosing Bias vs. Variance
先来看1个整体概括：
高偏差(欠拟合) —-High bias（underfit）
平衡(正好)—Just right
高方差（过拟合）—-High variance（overfit）

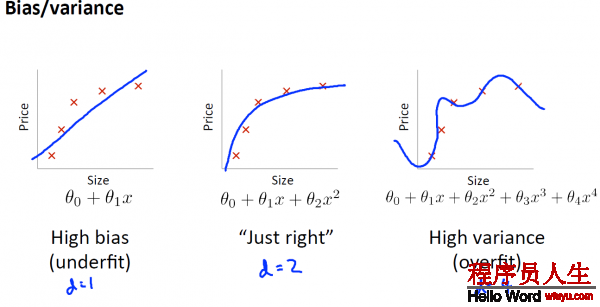
从下图，横轴表示多项式的次数d，纵轴表示误差error，我们可以看出，当d很小时，也就是处于underfit状态时，$J_{train}(\theta)$与$J_{CV}(\theta)$差不多大小，随着d增大，JCV 生活不易，码农辛苦
如果您觉得本网站对您的学习有所帮助,可以手机扫描二维码进行捐赠