您当前位置：首页 > php开源 > 综合技术 > 算法时间复杂度计算

算法时间复杂度计算

来源：程序员人生发布时间：2015-06-23 08:15:10 阅读次数：2871次

概述

??1个算法是由控制结构（顺序，分支，循环）和原操作（指固有数据类型的操作）构成。为了便于比较同1问题的不同算法，通常的做法是，从算法当选取1种对所研究的问题来讲是基本操作的原操作,以该基本原操作重复履行的次数作为算法的时间度量。多数情况下，基本原操作是它最深层循环中的原操作，对算法的时间度量最经常使用的是斟酌在最坏的情况下时间复杂度。

时间复杂度的定义

??算法中基本操作重复履行的次数是问题范围n的某个函数，用T(n)表示，若有某个辅助函数f(n)，使得当n趋近于无穷大时，T(n)/f(n)的极限值为不等于零的常数，则称f(n)是T(n)的同数量级函数。记作T(n)=O(f(n))，称O(f(n))为算法的渐进时间复杂度(O是数量级的符号 )，简称时间复杂度。

根据定义，可以归纳出基本的计算步骤

1. 计算出基本操作的履行次数T(n)
??基本操作即算法中的每条语句（以;号作为分割），语句的履行次数也叫做语句的频度。在做算法分析时，1般默许为斟酌最坏的情况。

2. 计算出T(n)的数量级
??求T(n)的数量级，只要将T(n)进行以下1些操作：疏忽常量、低次幂和最高次幂的系数。令f(n)=T(n)的数量级。

3. 用大O来表示时间复杂度
??当n趋近于无穷大时，如果lim(T(n)/f(n))的值为不等于0的常数，则称f(n)是T(n)的同数量级函数。记作T(n)=O(f(n))。

以上步骤可以简化

1. 找到履行次数最多的语句
2. 计算语句履行次数的数量级
3. 用大O来表示结果

举例

例1(O(n))

public void printsum(int count){
    int sum = 1;
    for(int i= 0; i<n; i++){
       sum += i;
    }   
    System.out.print(sum);
}

记住，只有可运行的语句才会增加时间复杂度，因此，上面方法里的内容除循环以外，其余的可运行语句的复杂度都是O(1)。
所以printsum的时间复杂度 = for的O(n)+O(1) = 疏忽常量 = O(n)

这里其实可以应用公式 num = n(n+1)/2，对算法进行优化，改成*

public void printsum(int count){
    int sum = 0;
    sum = count*(count+1)/2;
    System.out.print(sum);
}

这样算法的时间复杂度将由原来的O(n)降为O(1)，大大地提高了算法的性能。

例2（O(log2n)）

int i= 1;
while(i<n){
    i = i*2;
}

设(i=i*2)的频度是t, 则：2t(2的t次方)<=n; 两边去对数t<=log2n，斟酌最坏情况，取最大值t=log2n。T(n) = O(log2n)。
例3（O(n2)）

int num=0;
for(int i=0;i<n;i++){
    for(int j=0;j<n;j++){
        num++;
    }
}

时间复杂度为O(n2)。

经常使用算法的时间复杂度

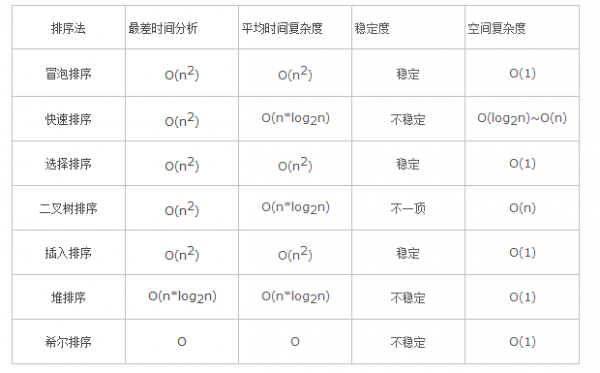
常用排序时间复杂度

参考

http://univasity.iteye.com/blog/1164707
http://www.cnblogs.com/songQQ/archive/2009/10/20/1587122.html

生活不易，码农辛苦
如果您觉得本网站对您的学习有所帮助,可以手机扫描二维码进行捐赠
程序员人生

------分隔线----------------------------

上一篇 shell学习笔记之八（函数）

下一篇 POJ 2763 Housewife Wind (树链剖分)

分享到:

------分隔线----------------------------

为码而活

积分：4237

15粉丝

7关注

栏目热点