【机器学习基础】验证

模型选择问题(Model Selection Problem)

我们在之前得知，通过最小化Ein来选择最好的模型不是1个正确的办法，由于这样可能会付出模型复杂度的代价、造成泛化效果差、造成过拟合的产生。
为了解决这个问题，我们的想法是找1些测试数据来看看哪一种模型对应测试数据的效果更好，但是用新的测试数据来作这个事情，实际上是做不到的掩耳盗铃的办法。
我们对照这两种方式，用训练数据来作选择的话，由于这些数据决定了终究的假定，所以再用这些训练数据来作验证的时候已被“污染”了；而如果用新的数据对测实验证的来讲，是“清洁”的。
折衷的办法是，将可用的数据留1小部份作为验证数据，当作模型选择的时候，再拿来用于验证。

验证

现在，我们从手中的数据拿出1小部份出来作验证数据，我们拿它来摹拟测试数据。为了将针对验证数据的毛病Eval和Eout联系起来，我们希望数据独立同散布于原始数据的散布；剩下的数据用作训练数据，可以用来做模型选择。

使用最好的Eval做模型选择

在做模型选择时，我们遵守以下流程，首先将数据集D分成两部份Dtrain和Dval，用Dtrain算出不同假定Hi的g-，再用Dval算出Ei，我们得到最小的Ei（记为Em）和其对应的假定Hm，再将所有的数据放在1起用Hm这个模型算出终究的模型参数gm（这个gm是用了最好的模型和最多的数据算出的结果，这会使得Eout最小）。

关系图形

我们用1个图形关系来表示不同的验证数据对真实误差Eout的影响。

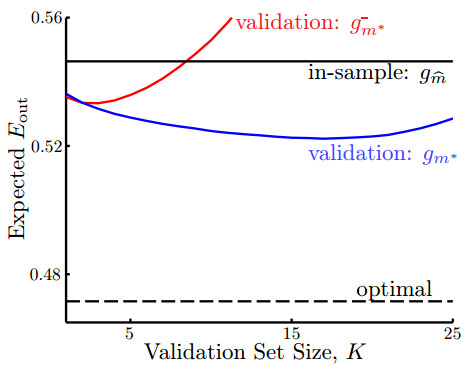
上面这个图的横轴是验证数据的大小是多少，纵轴表示Eout的大小。
其中红色的线代表用验证数据得到的终究假定g-，该假定不再用所有的数据重新做1次训练。
蓝色的线代表用验证数据得到了g-以后，在拿训练数据和验证数据放在1起做1次训练，得到的g。
不言而喻的是，蓝色的线总是比红色的线要低，并且蓝色的线比黑色的横线（表示直接用所有数据做训练得到的Ein）要低（这表示用验证数据得到的假定真的比不用验证数据得到的假定的误差要低）。
这说明，验证这个步骤确切是1个有用的方法。

那末为何红色的线有时候比Ein得到的g的毛病要大呢？
其解释是，如果验证数据变大，训练数据变小时，g-是用比较少的数据求出来的，所以g-的表现是不好的。用很少的数据选取的最好的g-有可能比起用全部数据训练得到的g还要差。

验证数据的大小

我们的决策根植于1个假定，我们要得到最后的假定g，所以希望Eout(g)和用验证数据得到Eout(g-)接近，另外还希望Eout(g-)和Eval(g-)接近。我们用Eval(g-)做选择，最后希望得到Eout(g)最好的那个假定。

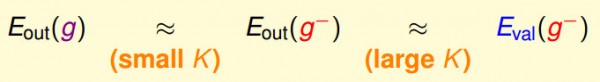
这两个近似等式需要的验证数据的数量是不同的，Eout(g-)≈Eval(g-)需要更多的验证数据，但这样会造成g-和g差很多（即上面的关系图形中，红色和蓝色的线在验证数据多的时候会差别很大）；Eout(g)≈Eout(g-)需要数量少的验证数据，但这是不太能肯定Eval和Eout是否是接近的。
实际上，验证数据量K=N/5，其中N是训练数据。

留1交叉验证

如果只有1个数据来作验证的话，那末其毛病Eval是：

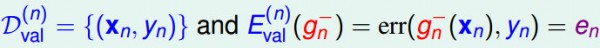
如果将所有的数据都拿来作验证的话，将其得到的结果平均起来，大概就可以告知我们Eout的情况：

理论保证

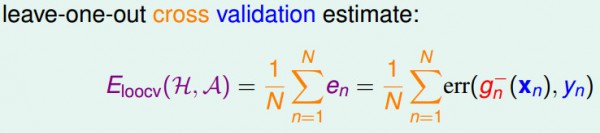
我们现在从偏理论的角度解释留1交叉检验的误差期望值和Eout(g-)的近似关系。
首先，我们假定对各式各样不同的数据集来作交叉检验并取1个平均。这里表示的都是leave-one-out交叉检验误差的期望值和Eout(g-)的期望值是差不多的。

实际利用

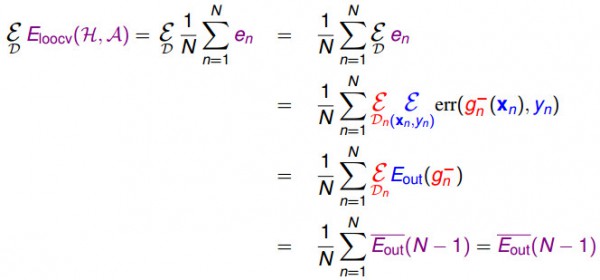
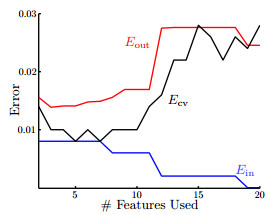
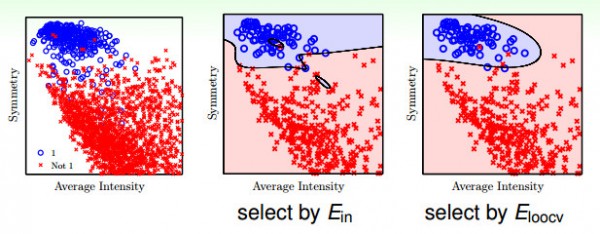
下图的横轴是特点转换的维度，从图中可以看出来，如果拿Ein来作选择，用尽可能多的特点可以做到尽量小的Ein，但是酿成的结果是过拟合，所以如果用较少的特点，Eout可能还小1点；如果用交叉检验的Ecv来作选择，其曲线和Eout的曲线很接近，所以就想下面第2个图中最右边的图象表示的，虽然会有1些错分类的情形，但是分类的曲线平滑很多，其在实际的表现就会更好。
这说明使用交叉验证的方法求得的假定可以比Ein得到的效果更好。

可能的问题

如果有1000个数据，我们用leave-one-out来作交叉验证的话，就需要做1000次来得到平均的误差，这样比较耗时，不太实际。

V折交叉检验

在留1交叉检验中，我们取1份数据来作验证，其余数据来作训练，
为了简单起见，我们可以将数据切成10部份，然后拿其中9份做训练，另外1份做验证，这样和留意交叉检验的效果是类似的。

常见的方式是将数据分成10份。
这类V折的交叉验证的方式比单1验证的方式更加稳定。

转载请注明作者Jason Ding及其出处
Github博客主页(http://jasonding1354.github.io/)
CSDN博客(http://blog.csdn.net/jasonding1354)
简书主页(http://www.jianshu.com/users/2bd9b48f6ea8/latest_articles)

生活不易，码农辛苦
如果您觉得本网站对您的学习有所帮助,可以手机扫描二维码进行捐赠