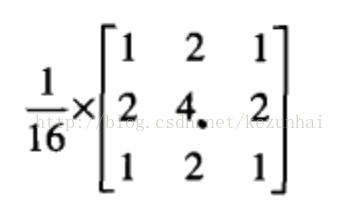PhotoShop算法实现进阶-模糊滤镜-高斯滤波(二十三)
来源:程序员人生 发布时间:2014-12-07 09:36:08 阅读次数:6090次
PhotoShop算法实现进阶-模糊滤镜-高斯滤波(2103)
kezunhai@gmail.com
http://blog.csdn.net/kezunhai
高斯模糊(Gaus Blur)采取2维高斯模板对图象进行模糊处理,用于图象模糊化(去除细节和噪声),它的处理效果给人1种更佳柔和的感觉。
1维高斯:
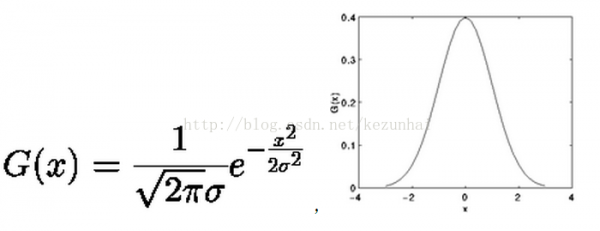
2维高斯:
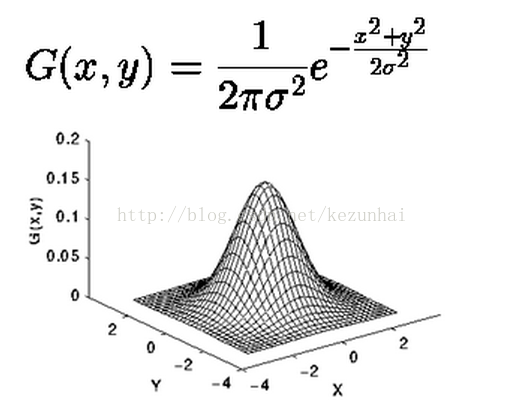
理论上,高斯散布在所有定义域上都有非负值,这就需要1个无穷大的卷积核。实际上,仅需要取均值周围3倍标准差内的值,之外部分直接去掉便可。 以下图为1个标准差为1.0的整数值高斯核:
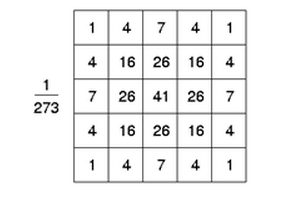
在有些场合,可以用下面的模块来对高斯核进行近似:
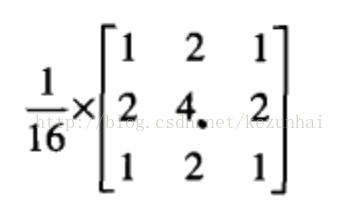
本文实现算法根据用户输入的核尺寸和方差来计算高斯核,实现高斯滤波,高斯核创建算法以下:
// 创建高斯核
// kSize:卷积核的大小3、5、7等(3×3、5×5、7×7)
// sigma:方差
void PhotoShop::CreateGaussKernel(float **pdKernel, int kSize, float sigma)
{
float dDis; //数组中1点到中心点距离
float dCenter = (kSize⑴)/2;
float dSum = 0;
float dValue;
int i, j;
//生成高斯数据
for ( i=0; i<kSize; i++)
{
for ( j=0; j<kSize; j++)
{
dDis = fabsf(i-dCenter) + fabsf(j-dCenter); // 用和来近似平方和的开方
dValue = exp(-dDis*dDis/(2*sigma*sigma+DBL_EPSILON));
pdKernel[i][j] = dValue;
dSum+=dValue;
}
}
//归1化
for ( i=0; i<kSize; i++)
{
for ( j=0; j<kSize; j++)
{
pdKernel[i][j] /= (dSum+DBL_EPSILON);
}
}
}
高斯滤波算法:
void PhotoShop::GaussianBlur(cv::Mat &img, cv::Mat &dst, int kSize, float sigma)
{
int height = img.rows;
int width = img.cols;
int chns = img.channels();
int i, j, k,p, q;
// 分配高斯核空间
float **pKernel = new float*[kSize];
for ( i=0; i<kSize; i++)
{
pKernel[i] = new float[kSize];
ZeroMemory(pKernel[i], kSize*sizeof(float));
}
CreateGaussKernel(pKernel, kSize, sigma); // 创建高斯核
if ( dst.empty())
dst.create(height, width, img.type());
float sum = 0;
int border = (kSize⑴)/2;
for ( i =border; i<height-border; i++)
{
unsigned char* dstData = (unsigned char*)dst.data + dst.step*i;
for ( j=border; j<width-border; j++)
{
for ( k=0; k<chns; k++)
{
sum = 0;
for ( p = -border; p<=border; p++)
{
for ( q = -border; q<=border; q++)
{
sum += getPixel(img, i+p, j+q, k)*pKernel[p+border][q+border];
}
}
dstData[j*chns+k] = saturate_cast<uchar>(sum+0.5);
} // for k
}
} // for i
}
算法测试:
高斯滤波由于其线性和良好的去噪效果,在很多算法中得到了广泛的利用,如Canny算子的预处理就采取了高斯滤波,OpenCV中的Sobel算子的实现也采取高斯滤波作为预处理步骤,还是闻名古今的SIFT算子采取了高斯金字塔和高斯差分来进行候选特点点的提取,有兴趣的朋友可以进1步深入了解高斯滤波的利用。
作者:kezunhai 出处:http://blog.csdn.net/kezunhai 欢迎转载或分享,但请务必声明文章出处。
生活不易,码农辛苦
如果您觉得本网站对您的学习有所帮助,可以手机扫描二维码进行捐赠