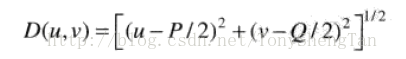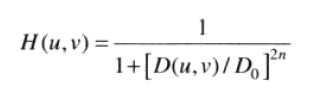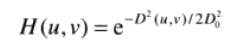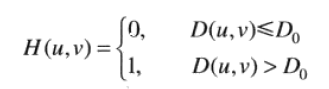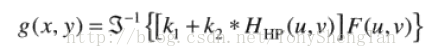灰度图像--频域滤波 滤波器
来源:程序员人生 发布时间:2015-01-24 09:07:47 阅读次数:4659次
学习DIP第26天
转载请标明本文出处:http://blog.csdn.net/tonyshengtan,欢迎大家转载,发现博客被某些论坛转载后,图象没法正常显示,没法正常表达本人观点,对此表示很不满意。有些网站转载了我的博文,很开心的是自己写的东西被更多人看到了,但不开心的是这段话被去掉了,也没标明转载来源,虽然这并没有版权保护,但感觉还是不太好,出于尊重文章作者的劳动,转载请标明出处!!!!
文章代码已托管,欢迎共同开发:https://github.com/Tony-Tan/DIPpro
开篇空话
仍然是空话开始,滤波器的起源就是频域来的,针对频域特性,滤波器被设计成各种各样的功能,但是频域滤波器都是线性的,转换到空域生成的卷积模板也是线性的,而有些从空域动身设计的滤波模板其实不是线性的,判断是否是线性可使用以下判断方法,也是信号与系统中经常使用的方法,F(ax+by)==aF(x)+bF(y)如果满足就是线性的,不满足则不是。常见的滤波模板中触及到排序的,都不是线性模板,而通过频域设计然后转换为空域模板的,都是线性的模板。
由于滤波原理上1篇中已做了详细的介绍,本篇主要记录几种常见的滤波器,并分析其滤波特点。主要介绍内容以下:
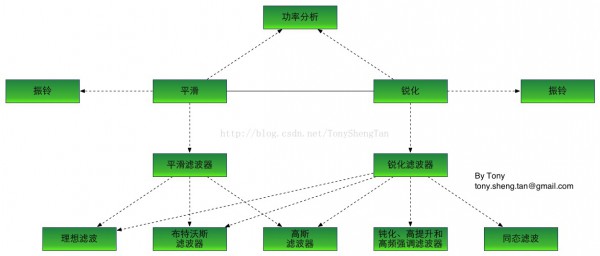
由于同态滤波的特殊性,将在下1篇中介绍,对每种滤波器,都会分析其功率和振铃现象。
现在给出1个经常使用的距离函数,将在所有下面所有滤波器中使用,使用欧氏距离,由于频率域的距离代表的是带宽,所以,截止频率,带宽意义重大(P,Q)为频谱大小,也是上篇中填充后的空域图象大小,并且我们使用的频谱都是中心化了的:
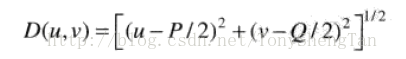
测试图片为:

平滑-低通滤波器
低通滤波器,顾名思义,只通太低频信号截断高频成份,在频谱中,中间部份为低频,4周为高频,截断点由滤波器的宽度决定,也就是截止频率,不同的截止频率对应于不同的效果和不同的剩余功率。
ILPF
理想低通滤波器,就是简单的截断,或说设置1个频率阈值,大于阈值的频谱置零,小于等于阈值的不变:

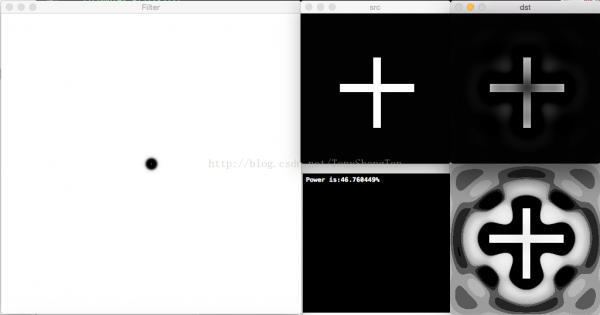
这个效果就是频域的1个圆形,我们来视察,频域截止频率为50,P,Q为512的ILPF:

下面来视察滤波器在截止频率为10,20,30的振铃和频率特性:
截止频率10,滤波后剩余功率50.196378%,有振铃:

截止频率20,滤波后剩余功率78.559714%,有振铃:
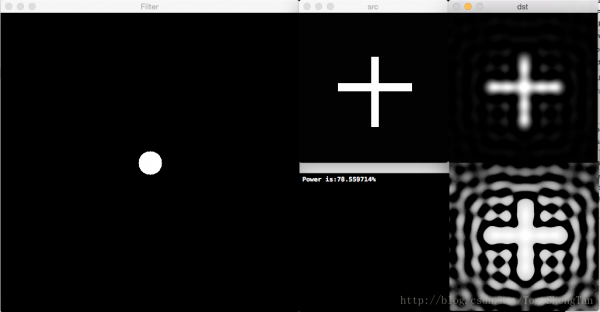
截止频率30,滤波后剩余功率88.736089%,有振铃:
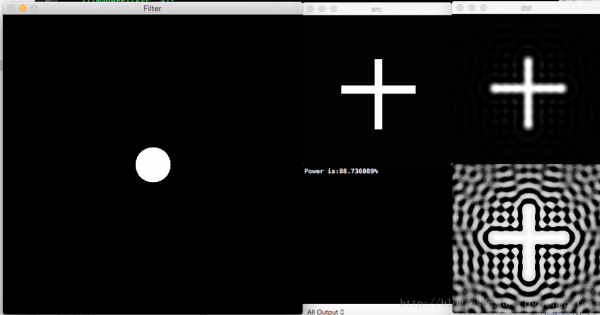
BLPF
布特沃斯低通滤波器,采取布特沃斯公式,产生1种低阶时转折平滑,高阶时转折尖锐的滤波器:
示意图以下:
下面视察2阶和10阶布特沃斯滤波器在截止频率10,20,30时的表现:
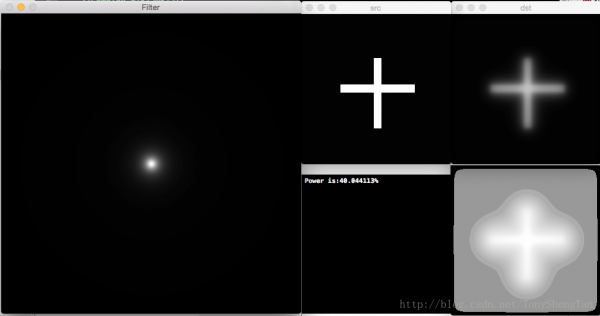
2阶:
截止频率10,滤波后剩余功率40.044113%,无振铃:
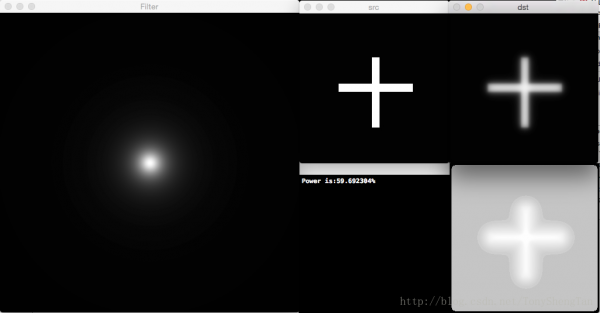
截止频率20,滤波后剩余功率59.692304%,无振铃:
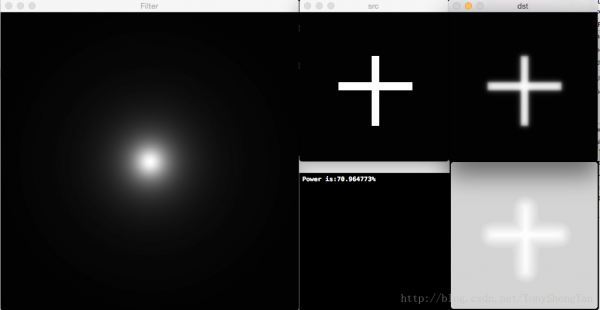
截止频率30,滤波后剩余功率70.964773%,无振铃:
10阶:
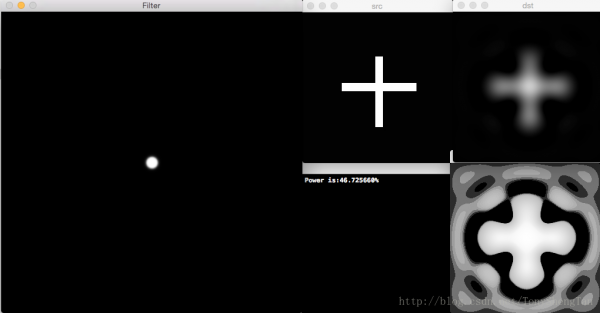
截止频率10,滤波后剩余功率46.72560%,有振铃:
截止频率20,滤波后剩余功率74.527332%,有振铃:
截止频率30,滤波后剩余功率86.566573%,有振铃:
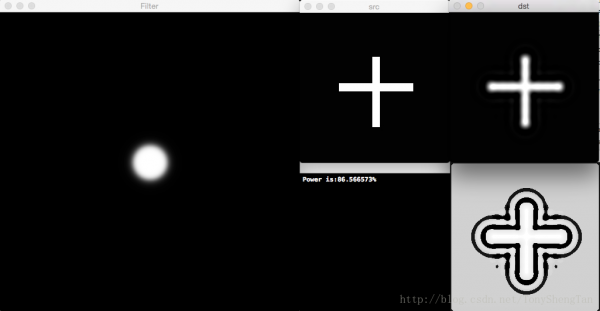
GLPF
由高斯公式产生的滤波器,由于高斯的傅里叶变换还是高斯的,所以变换无振铃效应:
滤波器示意图:
视察高斯滤波器在截止频率10,20,30时的表现:
截止频率10,滤波后剩余功率45036072%,无振铃:
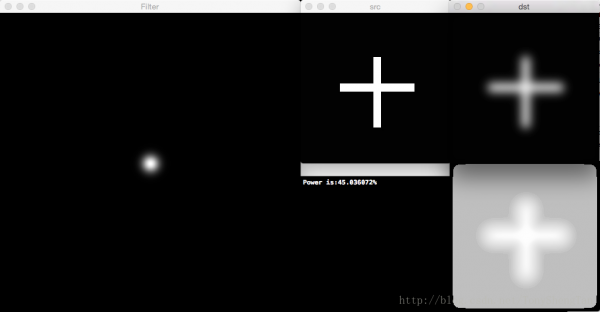
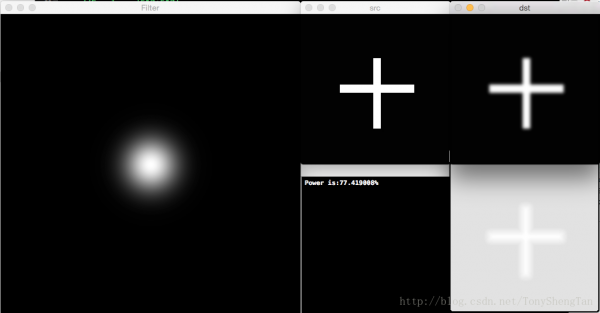
截止频率20,滤波后剩余功率66.908677%,无振铃:

截止频率30,滤波后剩余功率77.419008%,无振铃:
锐化-高通滤波器
与低频对应的就是高频滤波器,一样我们介绍理想高通,布特沃斯高通,高斯高通,并提出钝化高提升高频强调滤波器;
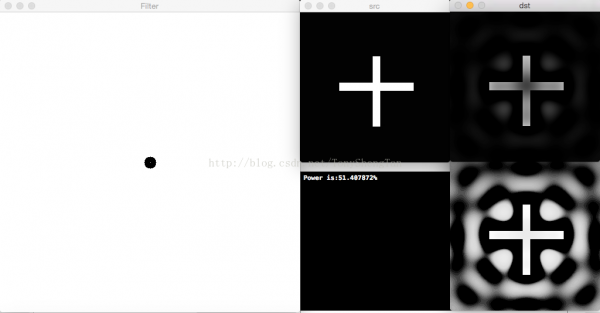
IHPF
理想高通的滤波器示意图:
一样视察截止频率为10,20,30的滤波效果和振铃效应:
截止频率10,滤波后剩余功率51.407872%,有振铃:
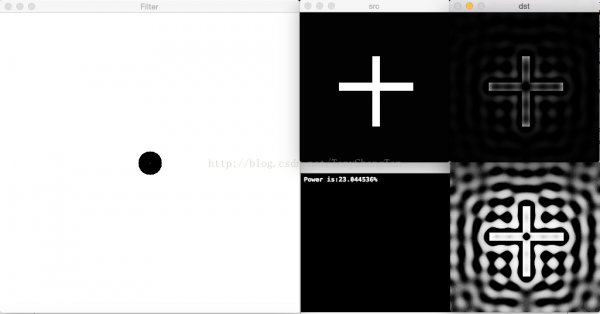
截止频率20,滤波后剩余功率23.044536%,有振铃:
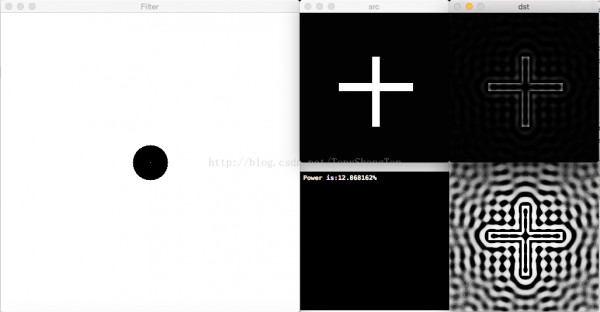
截止频率30,滤波后剩余功率12.868162%,有振铃:
BHPF
与低通布特沃斯相似,高通布特沃斯滤波器也是1种低阶时转折平滑,高阶时转折尖锐的滤波器

我们一样视察2阶和10阶的布特沃斯在截止频率为10,20,30时的效果和振铃现象:
2阶:
截止频率10,滤波后剩余功率34.679332%,无振铃:

截止频率20,滤波后剩余功率18.029713%,无振铃:
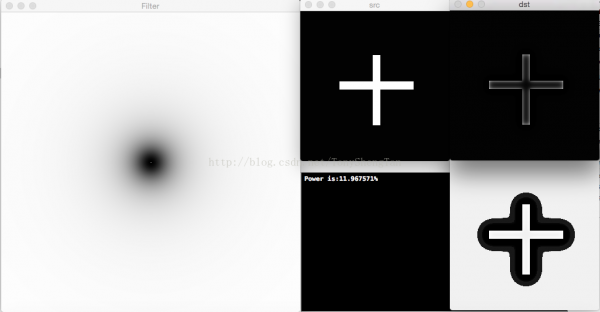
截止频率30,滤波后剩余功率11.967571%,无振铃:
10阶:
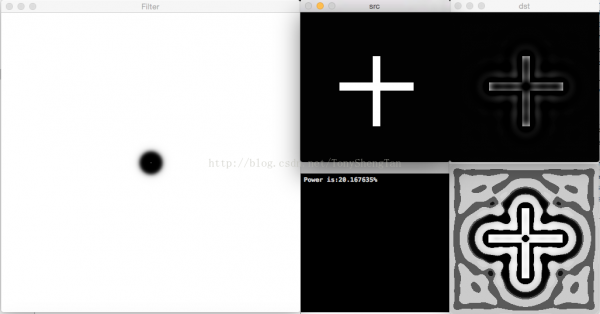
截止频率10,滤波后剩余功率46.760049%,有振铃:
截止频率20,滤波后剩余功率20.167635%,有振铃:
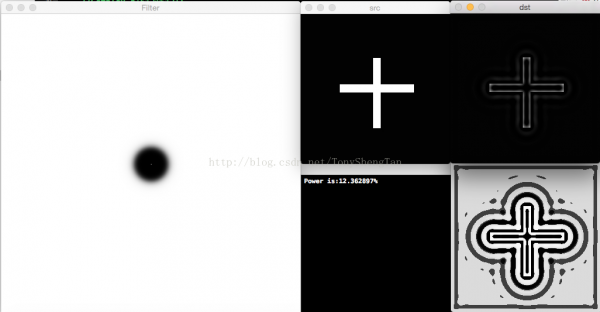
截止频率30,滤波后剩余功率12.362897%,有振铃:
GHPF
与低通1致,高斯高通滤波器为:
示意图:
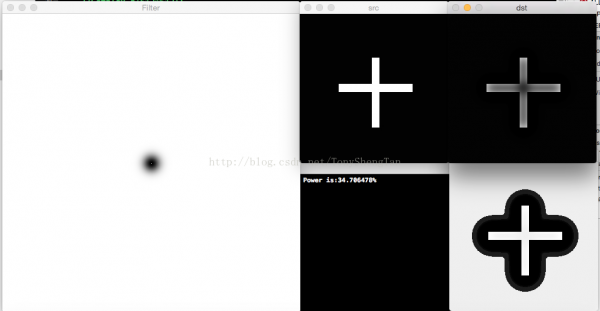
视察截止频率为10,20,30的滤波效果和振铃效应:
截止频率10,滤波后剩余功率34.706478%,无振铃:
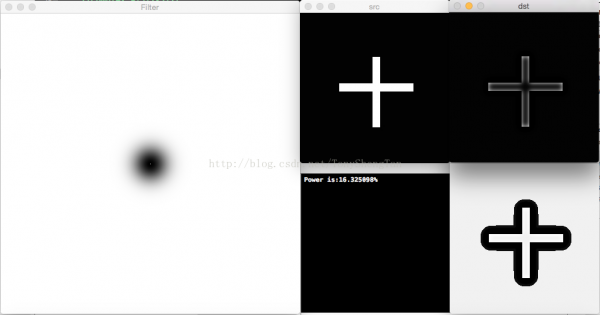
截止频率20,滤波后剩余功率16.325098%,无振铃:
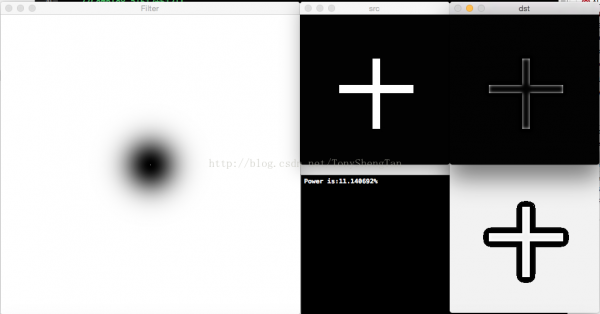
截止频率30,滤波后剩余功率11.140692%,无振铃:
部份代码
低通:
#include "lowpassfilter.h"
static double Distance(int x,int y,int c_x,int c_y){
return sqrt((x-c_x)*(x-c_x)+(y-c_y)*(y-c_y));
}
void IdealLPFilter(double *Filter,int width,int height,double cut_off_frequency){
int center_x=width/2;
int center_y=height/2;
double distance=0.0;
for(int i=0;i<width;i++)
for(int j=0;j<height;j++){
distance=Distance(i,j,center_x,center_y);
if(distance<=cut_off_frequency)
Filter[j*width+i]=1.0;
else
Filter[j*width+i]=0.0;
}
}
void ButterworthLPfilter(double *Filter,int width,int height,double cut_off_frequency,int n){
int center_x=width/2;
int center_y=height/2;
for(int i=0;i<width;i++)
for(int j=0;j<height;j++){
double value=1.0;
for(int k=0;k<n;k++)
value*=(Distance(i, j, center_x, center_y)/cut_off_frequency);
Filter[j*width+i]=1/(1+value);
}
}
void GaussianLPFilter(double *Filter,int width,int height,double cut_off_frequency){
int center_x=width/2;
int center_y=height/2;
for(int i=0;i<width;i++)
for(int j=0;j<height;j++){
double value=Distance(i, j, center_x, center_y);
Filter[j*width+i]=exp(-value*value/(2*cut_off_frequency*cut_off_frequency));
}
}
高通:
#include "highpassfilter.h"
static double Distance(int x,int y,int c_x,int c_y){
return sqrt((x-c_x)*(x-c_x)+(y-c_y)*(y-c_y));
}
void IdealHPFilter(double *Filter,int width,int height,double cut_off_frequency){
int center_x=width/2;
int center_y=height/2;
double distance=0.0;
for(int i=0;i<width;i++)
for(int j=0;j<height;j++){
distance=Distance(i,j,center_x,center_y);
if(distance<=cut_off_frequency)
Filter[j*width+i]=0.0;
else
Filter[j*width+i]=1.0;
}
Filter[width*(height+1)/2]+=1.0;
}
void ButterworthHPfilter(double *Filter,int width,int height,double cut_off_frequency,int n){
int center_x=width/2;
int center_y=height/2;
for(int i=0;i<width;i++)
for(int j=0;j<height;j++){
double value=1.0;
for(int k=0;k<n;k++)
value*=(Distance(i, j, center_x, center_y)/cut_off_frequency);
Filter[j*width+i]=1.0⑴.0/(1.0+value);
}
Filter[width*(height+1)/2]+=1.0;
}
void GaussianHPFilter(double *Filter,int width,int height,double cut_off_frequency){
int center_x=width/2;
int center_y=height/2;
for(int i=0;i<width;i++)
for(int j=0;j<height;j++){
double value=Distance(i, j, center_x, center_y);
Filter[j*width+i]=1.0-exp(-value*value/(2*cut_off_frequency*cut_off_frequency));
}
Filter[width*(height+1)/2]+=1.0;
}
钝化,高提升,高频强调
将高通滤波后的结果与原图进行1些加减,将得到钝化,高提升高频强调滤波器
对下面公式k1控制距离原点的偏移量,k2控制高频贡献。
- k1=1时k2=1为钝化模板
- k1=1时k2>1为高提升滤波器
- k1=1时,统称高频强调滤波器
具体性质据定于所选用的滤波模板,与上面叙述的模板性质和截止频率有关,在这里不详细叙述。
代码:
#include "Homomorphicfilter.h"
static double Distance(int x,int y,int c_x,int c_y){
return sqrt((x-c_x)*(x-c_x)+(y-c_y)*(y-c_y));
}
void HomorphicFilter(double *filter,int width,int height,double cut_off_frequency,double lambda_l,double lambda_h,double c){
int center_x=width/2;
int center_y=height/2;
double distance;
double distance_2;
double cut_off_frequency_2=cut_off_frequency*cut_off_frequency;
for(int i=0;i<height;i++)
for(int j=0;j<width;j++){
distance=Distance(j, i, center_x, center_y);
distance_2=distance*distance;
filter[i*width+j]=(lambda_h-lambda_l)*(1.0-exp(-c*distance_2/cut_off_frequency_2))+lambda_l;
}
}
总结
总结1下,这篇的理论在前面已介绍了,所以更多是验证前面的结论,视察滤波效果。滤波中值得注意的是振铃现象,对不能容忍人工缺点的利用中,如医学图象处理,不能使用带有振铃现象的滤波器,在实际物理中,理想滤波器没法实现,所以更多的使用高斯和其他1些无振铃的滤波器
生活不易,码农辛苦
如果您觉得本网站对您的学习有所帮助,可以手机扫描二维码进行捐赠