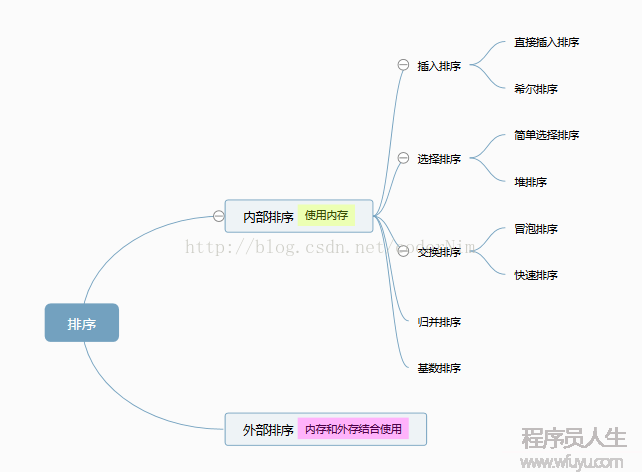
排序的分类:内部排序和外部排序
内部排序:数据记录在内存中进行排序
外部排序:因排序的数据量大,需要内存和外存结合使用进行排序
这里总结的8大排序是属于内部排序:
当n比较大的时候,应采取时间复杂度为(nlog2n)的排序算法:快速排序、堆排序或归并排序。
其中,快速排序是目前基于比较的内部排序中被认为最好的方法,当待排序的关键字是随机散布时,快速排序的平均时间最短。
———————————————————————————————————————————————————————————————————————
将1个记录插入到已排序好的有序表中,从而得到1个新的,记录数增1的有序表。
即:先将序列的第1个记录看成1个有序的子序列,然后从第2个记录逐一进行插入,直至全部序列有序为止。
要点:设立哨兵,用于临时存储和判断数组边界

插入排序是稳定的,由于如果1个带插入的元素和已插入元素相等,那末待插入元素将放在相等元素的后边,所以,相等元素的前后顺序没有改变。
#include<iostream>
using namespace std;
void print(int a[], int n ,int i)
{
cout<<i<<":";
for(int j= 0; j<8; j++){
cout<<a[j] <<" ";
}
cout<<endl;
}
void InsertSort(int a[],int n)
{
int i,j,tmp;
for(i=1;i<n;++i)
{
// 如果第i个元素大于第i⑴个元素,直接插入
// 否则
// 小于的话,移动有序表后插入
if(a[i]<a[i⑴])
{
j=i⑴;
tmp=a[i]; // 复制哨兵,即存储待排序元素
a[i]=a[i⑴]; // 前后移1个元素
while(tmp<a[j])
{
// 哨兵元素比插入点元素小,后移1个元素
a[j+1]=a[j];
--j;
}
a[j+1]=tmp; // 插入到正确的位置
}
print(a,n,i); // 打印每趟排序的结果
}
}
int main()
{
int a[8]={3,1,5,7,3,4,8,2};
print(a,8,0); // 打印原始序列
InsertSort(a,8);
return 0;
} 时间复杂度:O(n^2)
———————————————————————————————————————————————————————————————————————
先将全部待排序的记录序列分割成为若干子序列,分别进行直接插入排序,待全部序列中的记录“基本有序”时,再对全部记录顺次进行直接插入排序。
- 选择1个增量序列{ t1,t2,t3,...,tk }
- 按增量序列个数k,对序列进行k趟排序;
- 每趟排序,根据对应的增量ti,将待排序序列分割成若干长度为m的子序列,分别对各子序列进行直接插入排序。仅增量由于为1时,全部序列作为1个整表来处理,表长度即为全部序列的长度。
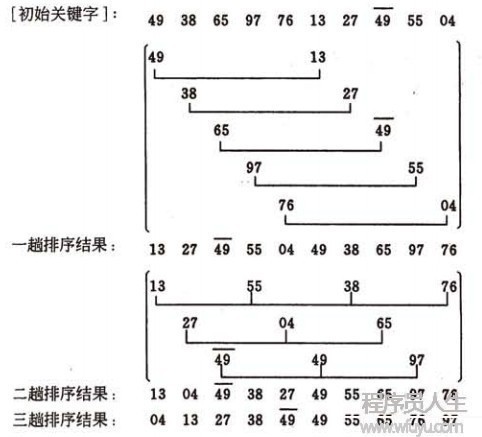
**如何选择增量序列?
简单选择:增量序列d = { n/2,n/4,n/8,...,1 } ,其中n为要排序数的个数。
#include<iostream>
using namespace std;
void print(int a[], int n)
{
for(int j= 0; j<8; j++){
cout<<a[j] <<" ";
}
cout<<endl;
}
void ShellInsertSort(int a[],int n,int dk)
{
int i,j,tmp;
for(i=dk;i<n;++i)
{
// 如果第i个元素大于第i-dk个元素,直接插入
// 否则
// 小于的话,移动有序表后插入
if(a[i]<a[i-dk])
{
j=i-dk;
tmp=a[i];
a[i]=a[i-dk]; // 复制哨兵,即存储待排序元素
while(tmp<a[j])
{
// 哨兵元素比插入点元素小,后移dk个元素
a[j+dk]=a[j];
j-=dk;
}
a[j+dk]=tmp; // 插入到正确的位置
}
}
}
void ShellSort(int a[],int n)
{
int dk=n/2;
while(dk>=1)
{
ShellInsertSort(a,n,dk);
dk/=2;
}
}
int main()
{
int a[8]={3,1,5,7,3,4,8,2};
print(a,8); // 打印原始序列
ShellSort(a,8);
print(a,8); // 打印排序后的序列
return 0;
}
可以发现,希尔排序是对简单插入排序算法的1种改进。
但希尔排序是不稳定的排序方法,由于排序进程中可能会改变相同元素在原始序列中的前后关系。
关于希尔排序的时效分析,取决于增量因子序列d的选取,特定情况下可以估算出关键码的比较次数和记录的移动次数。
目前还没有人给出选取最好的增量因子序列的方法。
———————————————————————————————————————————————————————————————————————
在要排序的1组数中,选出最小(或最大)的1个数与第1个位置的数进行交换;然后在剩下的数当中再找最小(或最大)的数与第2个位置的数交换,顺次类推,直到第n⑴个元素(倒数第2个数)和第n个元素(最后1个数)比较为止。
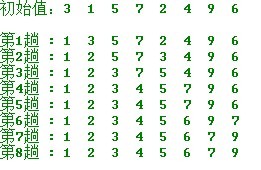
第1趟:从n个记录中找出关键码最小的记录与第1个记录交换;
第2趟:从第2个记录开始的n⑴个记录中再选出关键码最小的记录与第2个记录交换;
以此类推...
第 i 趟:从第i个记录开始的n-i+1个记录当选出关键码最小的记录与第i个记录交换,直至全部序列按关键码有序。
#include<iostream>
using namespace std;
void print(int a[], int n ,int i)
{
cout<<"第"<<i+1 <<"趟 : ";
for(int j= 0; j<8; j++){
cout<<a[j] <<" ";
}
cout<<endl;
}
// 返回数组的最小值的键值
int SelectMinKey(int a[],int n,int i)
{
int k=i;
for(int j=i+1;j<n;++j)
if(a[k]>a[j])
k=j;
return k;
}
void SelectSort(int a[],int n)
{
int key,tmp;
for(int i=0;i<n;++i)
{
key=SelectMinKey(a,n,i); // 选择最小的元素
if(key!=i)
{
// 最小元素与第i位置元素互换
tmp=a[i];
a[i]=a[key];
a[key]=tmp;
}
print(a,n,i);
}
}
int main()
{
int a[8]={3,1,5,7,3,4,8,2};
cout<<"原始序列:";
for(int i=0;i<8;++i)
{
cout<<a[i];
if(i==7)
cout<<endl;
else
cout<<" ";
}
SelectSort(a,8);
return 0;
}
———————————————————————————————————————————————————————————————————————
1)初始化堆;将数列[ 1 ... n ]构造成最大化堆
2)交换数据:将a[ 1 ]和a[ n ]交换,使a[ n ]是[ 1 ... n ]中的最大值;然后将[ 1 ... n⑴ ]重新调剂为最大堆。接着,将a[ 1 ]和a[ n⑴ ]交换,使a[ n⑴ ]是[ 1 ... n⑴ ]中的最大值;然后将[ 1 ... n⑵ ]重新调剂为最大堆。顺次类推,直到全部数列有序。
实现中用到了“数组实现的2叉堆的性质”。
在第1个元素的索引为0的情形中:
性质1:索引为i 的左孩子的索引是(2*i+1);
性质2:索引为i 的右孩子的索引是(2*i+2);
性质3:索引为i 的父节点的索引是floor( ( i⑴ ) / 2 );
下面演示对a={20,30,90,40,70,110,60,10,100,50,80}, n=11进行堆排序进程
数组a对应的初始结构:
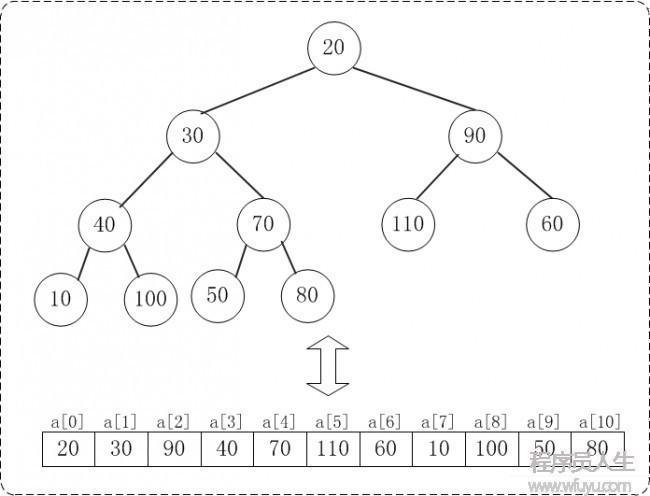
1 初始化堆:
在堆排序算法中,首先要将待排序的数组转换成最大堆。
下面演示将数组{20,30,90,40,70,110,60,10,100,50,80}转换为最大堆{110,100,90,40,80,20,60,10,30,50,70}的步骤。
1.1 i = n/2 - 1,即i = 4
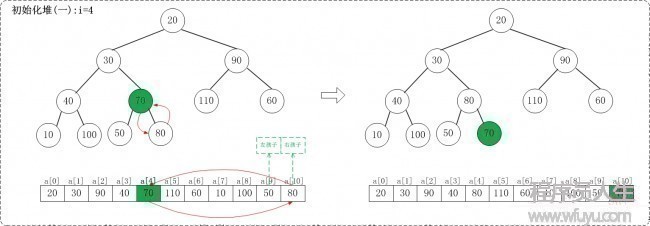
1.2 i = 3

1.3 i = 2
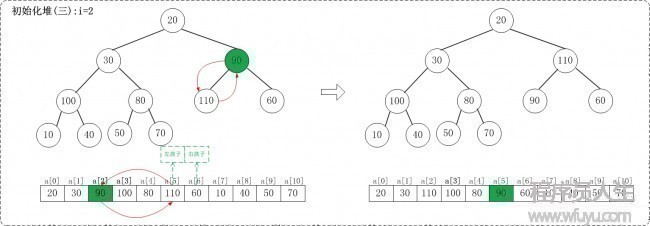
1.4 i = 1
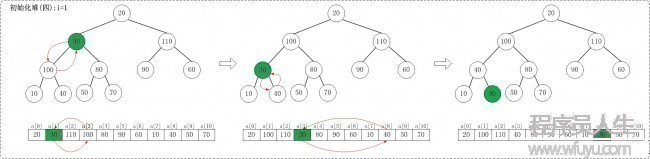
1.5 i = 0
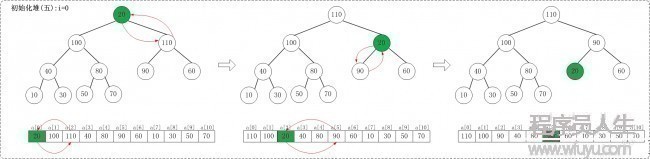
2 交换数据
在将数组转换成最大堆后,接着要进行交换数据,从而使数组成为1个真实的有序数组。
下面是当n = 10时交换数组的示意图:
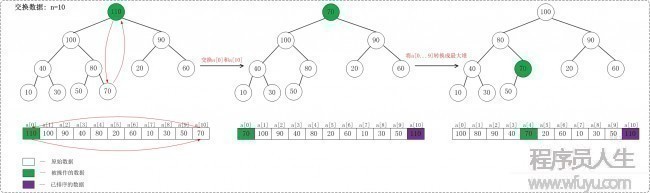
当n = 10时,首先交换a[0]和a[10],使得a[10]是a[0 ... 10 ]之间的最大值;然后调剂a[0 ... 9 ]使它成为最大堆。交换以后,a[10]是有序的;
当n = 9时,首先交换a[0]和a[9],使得a[9]是a[0 ... 9 ]之间的最大值;然后调剂a[0 ... 8 ]使它成为最大堆。交换以后,a[9]是有序的;
... ...
顺次类推,直到a[0 ... 10 ]是有序的。
#include<iostream>
using namespace std;
void maxheap_down(int a[],int start,int end)
{
int current=start; // 当前结点的位置
int left=2*current+1; // 左孩子的位置
int tmp=a[current]; // 当前节点的大小
for(;left<=end;current=left,left=2*left+1)
{
if(left<end&&a[left]<a[left+1])
++left; // 左右孩子当选择较大者
if(tmp>=a[left])
break; //调剂结束
else
{
// 交换值
a[current]=a[left];
a[left]=tmp;
}
}
}
void HeapSort(int a[],int n)
{
int i,tmp;
// 从(n/2⑴) --> 0逐次遍历。遍历以后,得到的数组实际上是1个(最大)2叉堆。
for(i=n/2⑴;i>=0;--i)
maxheap_down(a,i,n⑴);
// 从最后1个元素开始对序列进行调剂,不断的缩小调剂的范围直到第1个元素
for(i=n⑴;i>0;--i)
{
// 交换a[0]和a[i]。交换后,a[i]是a[0...i]中最大的
tmp=a[i];
a[i]=a[0];
a[0]=tmp;
// 调剂a[0...i⑴],使得a[0...i⑴]依然是1个最大堆;
// 即,保证a[i⑴]是a[0...i⑴]中的最大值
maxheap_down(a,0,i⑴);
}
}
int main()
{
int i;
int a[]={20,30,90,3,21,11,60,10,23,50,80};
int len=(sizeof(a))/(sizeof(a[0]));
cout<<"原始序列:";
for(i=0;i<len;++i)
cout<<a[i]<<" ";
cout<<endl;
HeapSort(a,len);
cout<<"堆排序后的序列:";
for(i=0;i<len;++i)
cout<<a[i]<<" ";
cout<<endl;
return 0;
}时间复杂度:O(nlog2n)
遍历1趟的时间复杂度是O(n);
堆排序是采取2叉堆进行排序的,2叉堆就是1棵2叉树,它需要遍历的次数就是2叉树的深度,而根据完全2叉树的定义,它的深度最少是log2(n+1),最多也不会超过log22n。因此,遍历次数介于log2(n+1)和log22n之间;因此得出它的时间复杂度是O(nlog2n)。
堆排序稳定性:不稳定的
它在交换数据的时候,是比较父节点和子节点之间的数据,所以即便是存在两个数值相等的兄弟结点,它们的相对顺序在排序中也可能产生变化。
———————————————————————————————————————————————————————————————————————
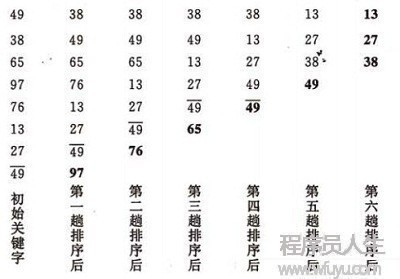
在要排序的1组数中,对当前还未排好序的范围内的全部数,自上而下对相邻的两个数顺次进行比较和调剂,让较大的数往下沉,较小的数往上冒。
即:每当相邻的数比较后发现它们的顺序与排序要求相反时,就将它们互换。
#include<iostream>
using namespace std;
void print(int a[], int n ,int i)
{
cout<<"第"<<i+1<<"趟 : ";
for(int j= 0; j<8; j++){
cout<<a[j]<<" ";
}
cout<<endl;
}
void BubbleSort(int r[],int size)
{
int i,j,temp;
bool exchange; //交换标志
for(i=0;i<size;i++)
{
exchange=false; //本趟排序开始前,交换标志设为假
for(j=size⑴;j>=i;--j)
if(r[j]<r[j⑴])
{
temp=r[j]; //暂存单元
r[j]=r[j⑴];
r[j⑴]=temp;
exchange=true; //产生了交换,故将交换标志置为真
}
if(!exchange) //本趟没有产生交换,提早终止算法
return;
print(r,size,i);
}
}
int main()
{
int r[8]={3,1,5,7,3,4,8,2};
cout<<"原始序列:";
for(int i=0;i<8;i++)
{
cout<<r[i];
if(i==7)
cout<<endl;
else
cout<<" ";
}
BubbleSort(r,8);
return 0;
}
———————————————————————————————————————————————————————————————————————
1)选择1个基准元素,通常选择第1个元素或最后1个元素
2)通过1趟排序将待排序的记录分割成独立的两部份,其中1部份记录的元素值均比基准元素值小,另外一部份记录的元素值比基准值大。
3)此时基准元素在其排好序后的正确位置
4)然后分别对这两部份记录用一样的方法继续进行排序,直到全部序列有序
a)1趟排序的进程:

b)排序的全进程:

#include<iostream>
using namespace std;
int Partition(int r[],int first,int end)
{
int i=first,j=end,temp; //初始化
while(i<j)
{
//j从后向前扫描,直到r[j]<r[i],将r[j]移动到r[i]的位置,使关键码小(同轴值相比)的记录移动到前面去;
while(i<j && r[i]<=r[j]) --j; //右边扫描
if(i<j)
{
//将较小记录交换到前面
temp=r[i];
r[i]=r[j];
r[j]=temp;
++i;
}
//i从前向后扫描,直到r[i]>r[j],将r[i]移动到r[j]的位置,使关键码大(同轴值相比)的记录移动到后面去;
while(i<j && r[i]<=r[j]) ++i; //左边扫描
if(i<j)
{
//将较大记录交换到后面
temp=r[i];
r[i]=r[j];
r[j]=temp;
--j;
}
//重复上述进程,直到i=j
}
return i;
}
void QuickSort(int r[],int first,int end)
{
if(first<end)
{
int pivotpos=Partition(r,first,end); //1次划分
QuickSort(r,first,pivotpos⑴); //对前1个子序列进行快速排序
QuickSort(r,pivotpos+1,end); //对后1个子序列进行快速排序
}
}
int main()
{
int r[8]={3,1,5,7,3,4,8,2};
cout<<"原始序列:";
for(int i=0;i<8;i++)
{
cout<<r[i];
if(i==7)
cout<<endl;
else
cout<<" ";
}
QuickSort(r,0,7);
cout<<"排序后的序列:";
for(int i=0;i<8;i++)
{
cout<<r[i];
if(i==7)
cout<<endl;
else
cout<<" ";
}
return 0;
}快速排序通常被认为在同数量级(O(nlog2n)中平均性能最好的。但如果初始序列按关键码有序或基本有序时,快速排序反而退化为冒泡排序。
为改进之,通常以“3者取中法“来选取基准记录,行将排序区间的两个端点与中点3个记录关键码居中地调剂为支点记录。
快速排序是1个不稳定的排序算法。
———————————————————————————————————————————————————————————————————————
归并排序是将两个(或两个以上)的有序表合并成1个新的有序表,行将待排序序列分为若干个子序列,每一个序列是有序的。然后再将有序子序列合并为整体有序序列。
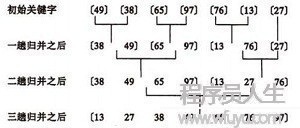
1个元素的表总是有序的,所以对n个元素的待排序列,每一个元素可看成1个有序子表。对子表两两合并,生成n/2个子表,所得子表除最后1个子表长度可能为1外,其余子表长度均为2。再进行两两合并,直到生成n个元素按关键码有序的表。
#include<iostream>
using namespace std;
void print(int a[], int n)
{
for(int j=0; j<n; j++){
cout<<a[j] <<" ";
}
cout<<endl;
}
void merge(int r[],int left,int mid,int right)
{
int *rf=new int[right-left+1]; //汇总2个有序区的临时数组
int i=left; // 第1个有序区的索引
int j=mid+1; // 第2个有序区的索引
int k=0; // 临时区域的索引
while(i<=mid&&j<=right)
{
if(r[i]<r[j])
{
rf[k++]=r[i++];
}
else
{
rf[k++]=r[j++];
}
}
while(i<=mid)
rf[k++]=r[i++];
while(j<=right)
rf[k++]=r[j++];
// 将排序后的元素,全部都整合到数组a中。
for(i=0;i<k;i++)
r[left + i] = rf[i];
delete []rf;
}
void MergeSort(int r[],int left,int right)
{
if(r!=NULL&&left<right)
{
int mid=(left+right)/2;
MergeSort(r,left,mid); // 递归排序a[start...mid]
MergeSort(r,mid+1,right); // 递归排序a[mid+1...end]
// a[start...mid] 和 a[mid...end]是两个有序空间,
// 将它们排序成1个有序空间a[start...end]
merge(r,left,mid,right);
}
}
int main()
{
int r[9]={32, 21, 67, 11, 5, 43, 99, 18,12};
cout<<"原始序列:";
print(r,9);
MergeSort(r,0,8);
cout<<"归并排序后的序列:";
print(r,9);
return 0;
} 归并排序的时间复杂度是O(nlog2n)
归并排序的情势就是1颗2叉树,它需要遍历的次数就是2叉树的深度,而根据完全2叉树的深度可以得出它的时间复杂度是O(nlog2n)。
归并排序是稳定的算法,它满足稳定算法的定义。
———————————————————————————————————————————————————————————————————————
将数组分到有限数量的桶子里;
假定待排序的数组a中共有n个整数,并且已知数组a中的数据大小范围是[ 0 , MAX ) 。在桶排序时,创建容量为MAX的桶数组r,并将桶数组的元素都初始化为0;将容量为MAX的桶数组中的每个单元都看成1个“桶”。
在排序时,逐一遍历数组a,将数组a的值作为“桶数组r”的下标。当a中的数据被读取时,就将相应的桶的值加1。例如,读取到数组a[3]=5,就将r[5]的值+1。
假定a={8,2,3,4,3,6,6,3,9}, max=10。此时,将数组a的所有数据都放到需要为0⑼的桶中。以下图:
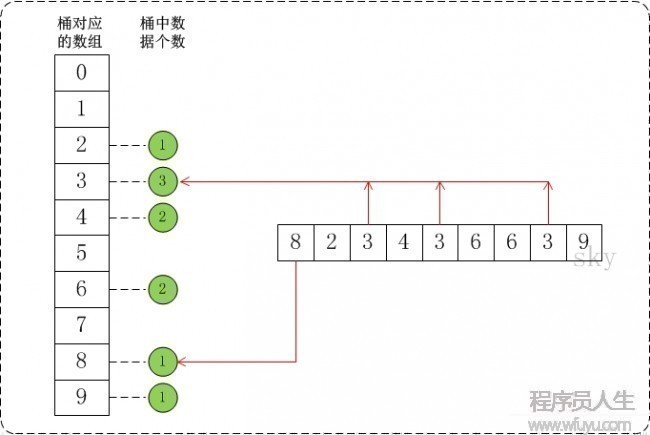
在将数据放到桶中以后,再通过1定算法将桶中的数据提出来并转换成有序数组,这就得到我们需要的有序序列。
#include<iostream>
#include<cstring> // memset头文件
using namespace std;
void BucketSort(int a[],int n,int max)
{
int i,j;
int buckets[max];
// 将buckets中的所有数据都初始化为0
memset(buckets,0,max*sizeof(int));
// 计数
for(i=0;i<n;++i)
++buckets[a[i]];
// 排序
for(i=0,j=0;i<max;++i)
while((buckets[i]--)>0)
a[j++]=i;
}
int main()
{
int i;
int a[] = {8,2,1,4,3,7,6,3,9};
int len = (sizeof(a))/(sizeof(a[0]));
cout<<"原始序列:";
for(i=0;i<len;++i)
cout<<a[i]<<" ";
cout<<endl;
BucketSort(a,len,10);
cout<<"堆排序后的序列:";
for(i=0;i<len;++i)
cout<<a[i]<<" ";
cout<<endl;
return 0;
}—————————————————————————————————————————————————————————————————————————————
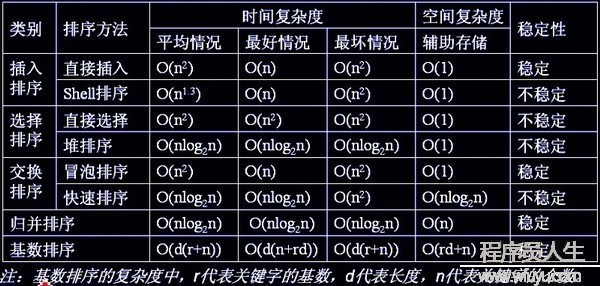
各种排序的稳定性,时间复杂度和空间复杂度总结:
对n较大的排序记录。1般的选择都是时间复杂度为O(nlog2n)的排序方法。
