《剑指offer》:[59]对称的二叉树
来源:程序员人生 发布时间:2016-08-29 08:30:01 阅读次数:2528次
题目;请实现1个函数,用来判断1棵2叉树是否是对称的。如果1颗2叉树和它的镜像1样,那末它是对称的。
例如,下面2棵树图(1)就是对称的2叉树,而图(2)(3)就不是的。
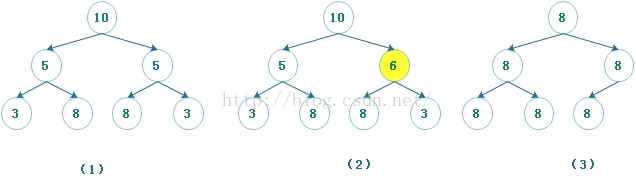
分析:我们知道树的遍历有3种方式:前,中,后。顾名思义,对称就是左侧的和右侧的相等,中间的自己等于自己。
所以我们自己可以定义1种对称遍历算法,例如前序遍历中的前,左,右。对称算法就是:前,右,左。恰好对称比较。固然了其他的中和后序遍历也行,我们也能够定义与其对应的对称算法。
但是其中为了不出现树(3)中的遍历出来的数据1样,造成误判,我们需要对叶子结点加上标识,如空节点需要设置为NULL。而不能只是比较遍历后的数据。
具体是实现代码以下:
#include <iostream>
using namespace std;
struct BinaryTree
{
int data;
BinaryTree *pLeft;
BinaryTree *pRight;
};
BinaryTree *pRoot1=NULL;
BinaryTree *pRoot2=NULL;
BinaryTree *pRoot3=NULL;
void CreateTree(BinaryTree * &root)
{
int data;
cin>>data;
if(0==data)
root=NULL;
else
{
root=new BinaryTree;
root->data=data;
//前序遍历构建2叉树;
CreateTree(root->pLeft);
CreateTree(root->pRight);
}
}
bool IsSymmetricalHelp(BinaryTree *root1,BinaryTree *root2)
{
if(root1==NULL && root2==NULL)
return true;
if(root1==NULL || root2==NULL)//把null也算上,很重要,避免数据1样的特殊情况;
return false;
if(root1->data!=root2->data)
return false;
return IsSymmetricalHelp(root1->pLeft,root2->pRight)
&& IsSymmetricalHelp(root1->pRight,root2->pLeft);
}
bool IsSymmetrical(BinaryTree *root)
{
return IsSymmetricalHelp(root,root);
}
void PreOrder(BinaryTree *root)
{
if(root)
{
cout<<root->data<<" ";
PreOrder(root->pLeft);
PreOrder(root->pRight);
}
}
void UntiPreOrder(BinaryTree *root)
{
if(root)
{
cout<<root->data<<" ";
PreOrder(root->pRight);
PreOrder(root->pLeft);
}
}
int main()
{
bool result=false;
CreateTree(pRoot1);
cout<<"树1的--前序遍历:";
PreOrder(pRoot1);
cout<<endl;
cout<<"树1的反前序遍历:";
UntiPreOrder(pRoot1);
result=IsSymmetrical(pRoot1);
if(result)
cout<<endl<<"该树是对称树!"<<endl;
else
cout<<"该树不是对称树!"<<endl;
cout<<endl;
CreateTree(pRoot2);//树3虽然遍历1样,但是否是对成树!
cout<<"树2的--前序遍历:";
PreOrder(pRoot2);
cout<<endl;
cout<<"树2的反前序遍历:";
UntiPreOrder(pRoot2);
cout<<endl;
result=IsSymmetrical(pRoot2);
if(result)
cout<<"该树是对称树!"<<endl;
else
cout<<"该树不是对称树!"<<endl;
cout<<endl;
system("pause");
return 0;
}
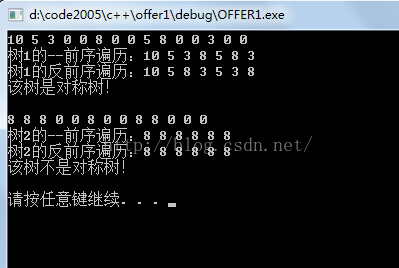
运行结果以下;
生活不易,码农辛苦
如果您觉得本网站对您的学习有所帮助,可以手机扫描二维码进行捐赠



