013--Floyd算法-动态规划-《算法设计技巧与分析》M.H.A学习笔记
来源:程序员人生 发布时间:2016-07-07 13:57:46 阅读次数:2531次
多源最短路:有向图,求从每一个顶点到其他所有顶点的最短距离。
基本思路:
假定有向图的所有点编号为1到n,l[i,j]表示从i到j的边的长度,如果不存在边,则置为正无穷。
定义d(k,i,j)表示从点i到点j,并且不经过编号大于k的点的最短距离。
初始化条件:
K=0时,d(0,i,j)=l[i,j]。
状态转移方程:
d(k,i,j)=min{ d(k⑴,i,j),d(k⑴,i,k)+d(k⑴,k,j) } 1<=k<=n
因而我们有以下的递归式:
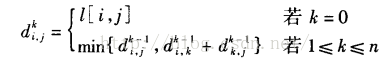
算法分析:
明显,Floyd算法的时间复杂度是Θ(n3),空间复杂度是Θ(n2)。
伪代码:


C++代码:
for( int k = 1; k <= n; ++k )
for( int i = 1; i <= n; ++i )
for( int j = 1; j <= n; ++j )
d[i][j]=min(d[i][j],d[i][k]+d[k][j]);
生活不易,码农辛苦
如果您觉得本网站对您的学习有所帮助,可以手机扫描二维码进行捐赠