您当前位置：首页 > php开源 > php教程 > 基于Python3 神经网络的实现

基于Python3 神经网络的实现

来源：程序员人生发布时间：2016-07-05 14:52:40 阅读次数：4747次

基于Python3 神经网络的实现

本次学习是Denny Britz（作者）的Python2神经网络项目修改成基于Python3实现的神经网络（本篇博文代码完全）。重在理解原理和实现方法，部份翻译不够准确，可查看Python2版的原文。原文英文地址（基于Python2）

概述如何搭建开发环境

安装Python3、安装jupyter notebook和其他科学栈如numpy

pip install jypyter notebook
pip install numpy

生成测试数据集

# 导入需要的包
import matplotlib.pyplot as plt
import numpy as np
import sklearn
import sklearn.datasets
import sklearn.linear_model
import matplotlib

# Display plots inline and change default figure size
%matplotlib inline
matplotlib.rcParams['figure.figsize'] = (10.0, 8.0)

生成数据集

make_moons数据集生成器

# 生成数据集并绘制出来
np.random.seed(0)
X, y = sklearn.datasets.make_moons(200, noise=0.20)
plt.scatter(X[:,0], X[:,1], s=40, c=y, cmap=plt.cm.Spectral)

<matplotlib.collections.PathCollection at 0x1e88bdda780>

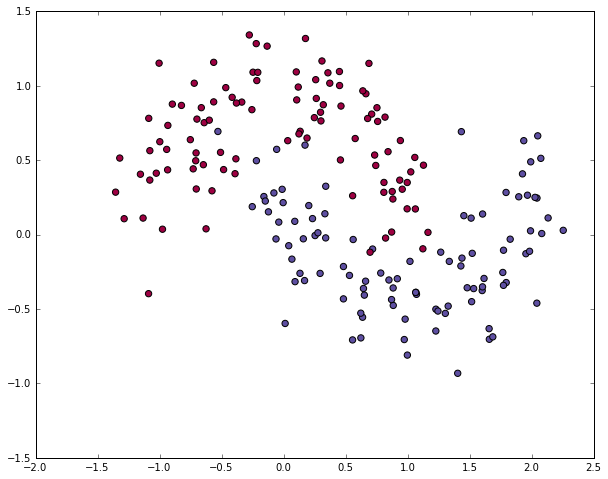
这里写图片描述

逻辑回归

为了证明（学习特点）这点，让我们来训练1个逻辑回归分类器吧。以x轴，y轴的值为输入，它将输出预测的类（0或1）。为了简单起见，这儿我们将直接使用scikit-learn里面的逻辑回归分类器。

# 训练逻辑回归训练器
clf = sklearn.linear_model.LogisticRegressionCV()
clf.fit(X, y)

LogisticRegressionCV(Cs=10, class_weight=None, cv=None, dual=False,
           fit_intercept=True, intercept_scaling=1.0, max_iter=100,
           multi_class='ovr', n_jobs=1, penalty='l2', random_state=None,
           refit=True, scoring=None, solver='lbfgs', tol=0.0001, verbose=0)

# Helper function to plot a decision boundary.
# If you don't fully understand this function don't worry, it just generates the contour plot below.
def plot_decision_boundary(pred_func):
    # Set min and max values and give it some padding
    x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
    y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
    h = 0.01
    # Generate a grid of points with distance h between them
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
    # Predict the function value for the whole gid
    Z = pred_func(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    # Plot the contour and training examples
    plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)
    plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Spectral)

# Plot the decision boundary
plot_decision_boundary(lambda x: clf.predict(x))
plt.title("Logistic Regression")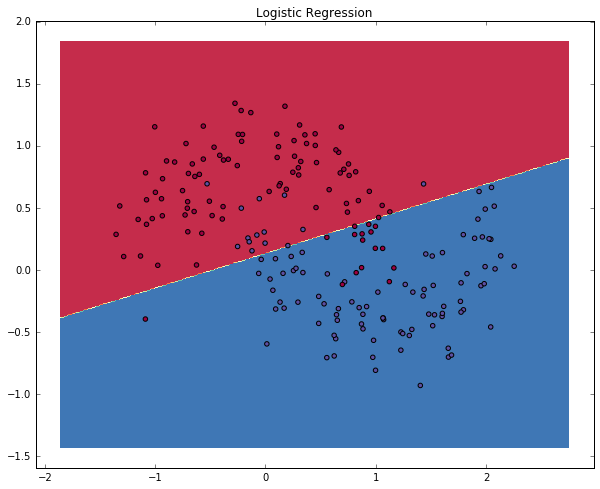

这里写图片描述

The graph shows the decision boundary learned by our Logistic Regression classifier. It separates the data as good as it can using a straight line, but it’s unable to capture the “moon shape” of our data.

训练1个神经网络

现在，我们搭建由1个输入层，1个隐藏层，1个输出层组成的3层神经网络。输入层中的节点数由数据的维度来决定，也就是2个。相应的，输出层的节点数则是由类的数量来决定，也是2个。（由于我们只有1个预测0和1的输出节点，所以我们只有两类输出，实际中，两个输出节点将更容易于在后期进行扩大从而取得更多种别的输出）。以x，y坐标作为输入，输出的则是两种几率，1种是0（代表女），另外一种是1（代表男）。结果以下：

神经网络作出预测原理

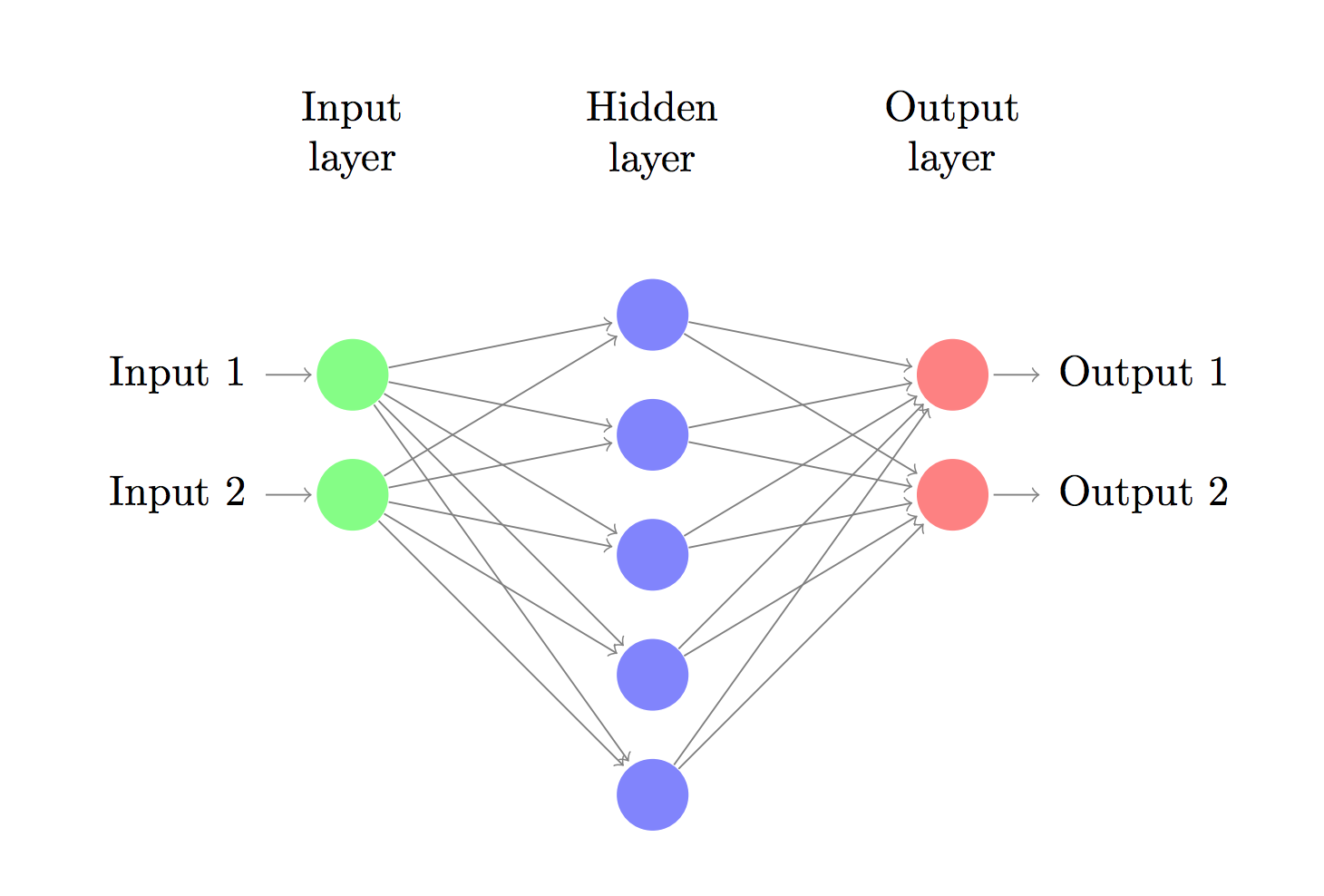
神经网络通过前向传播做出预测。前向传播仅仅是做了1堆矩阵乘法并使用了我们之前定义的激活函数。如果该网络的输入x是2维的，那末我们可以通过以下方法来计算其预测值：

z 1 a 1 z 2 a 2 = x W 1 + b 1 = tanh (z 1) = a 1 W 2 + b 2 = y^= s o f t m a x (z 2)

zi is the input of layer i and ai is the output of layer i after applying the activation function. W1,b1,W2,b2 are parameters of our network, which we need to learn from our training data. You can think of them as matrices transforming data between layers of the network. Looking at the matrix multiplications above we can figure out the dimensionality of these matrices. If we use 500 nodes for our hidden layer then W1∈R2×500, b1∈R500, W2∈R500×2, b2∈R2. Now you see why we have more parameters if we increase the size of the hidden layer.

研究参数

Learning the parameters for our network means finding parameters (W1,b1,W2,b2) that minimize the error on our training data. But how do we define the error? We call the function that measures our error the loss function. A common choice with the softmax output is the cross-entropy loss. If we have N training examples and C classes then the loss for our prediction y^ with respect to the true labels y is given by:

L (y, y^) = - 1 N \sum n \in N \sum i \in C y n, i log y^n, i

The formula looks complicated, but all it really does is sum over our training examples and add to the loss if we predicted the incorrect class. So, the further away y (the correct labels) and y^ (our predictions) are, the greater our loss will be.

Remember that our goal is to find the parameters that minimize our loss function. We can use gradient descent to find its minimum. I will implement the most vanilla version of gradient descent, also called batch gradient descent with a fixed learning rate. Variations such as SGD (stochastic gradient descent) or minibatch gradient descent typically perform better in practice. So if you are serious you’ll want to use one of these, and ideally you would also decay the learning rate over time.

As an input, gradient descent needs the gradients (vector of derivatives) of the loss function with respect to our parameters: ∂L∂W1 生活不易，码农辛苦
如果您觉得本网站对您的学习有所帮助,可以手机扫描二维码进行捐赠
程序员人生

------分隔线----------------------------

上一篇 bzoj4565【HAOI2016】字符合并

下一篇 Android中listView的下拉加载功能实现

分享到:

------分隔线----------------------------

为码而活

积分：4237

15粉丝

7关注

栏目热点