数据结构例程――用二叉树遍历思想解决问题

本文是数据结构基础系列(6)：树和2叉树中第10课时2叉树的遍历的例程。

【利用2叉树遍历思想解决问题】(请利用2叉树算法库)
　　假定2叉树采取2叉链存储结构存储，分别实现以下算法，并在程序中完成测试：
　　（1）计算2叉树节点个数；
　　（2）输出所有叶子节点；
　　（3）求2叉树b的叶子节点个数
　　（4）设计1个算法Level(b,x,h)，返回2叉链b中data值为x的节点的层数。
　　（5）判断2叉树是不是类似（关于2叉树t1和t2类似的判断：①t1和t2都是空的2叉树，类似；②t1和t2之1为空，另外一不为空，则不类似；③t1的左子树和t2的左子树是类似的，且t1的右子树与t2的右子树是类似的，则t1和t2类似。）

［参考解答］（btreee.h见算法库）
　　（1）计算2叉树节点个数；

#include #include "btree.h" int Nodes(BTNode *b) { if (b==NULL) return 0; else return Nodes(b->lchild)+Nodes(b->rchild)+1; } int main() { BTNode *b; CreateBTNode(b,"A(B(D,E(H(J,K(L,M(,N))))),C(F,G(,I)))"); printf("2叉树节点个数: %d ", Nodes(b)); DestroyBTNode(b); return 0; }

（2）输出所有叶子节点；

#include <stdio.h> #include "btree.h" void DispLeaf(BTNode *b) { if (b!=NULL) { if (b->lchild==NULL && b->rchild==NULL) printf("%c ",b->data); else { DispLeaf(b->lchild); DispLeaf(b->rchild); } } } int main() { BTNode *b; CreateBTNode(b,"A(B(D,E(H(J,K(L,M(,N))))),C(F,G(,I)))"); printf("2叉树中所有的叶子节点是: "); DispLeaf(b); printf(" "); DestroyBTNode(b); return 0; }

（3）求2叉树b的叶子节点个数

#include <stdio.h> #include "btree.h" int LeafNodes(BTNode *b) //求2叉树b的叶子节点个数 { int num1,num2; if (b==NULL) return 0; else if (b->lchild==NULL && b->rchild==NULL) return 1; else { num1=LeafNodes(b->lchild); num2=LeafNodes(b->rchild); return (num1+num2); } } int main() { BTNode *b; CreateBTNode(b,"A(B(D,E(H(J,K(L,M(,N))))),C(F,G(,I)))"); printf("2叉树b的叶子节点个数: %d ",LeafNodes(b)); DestroyBTNode(b); return 0; }

（4）设计1个算法Level(b,x,h)，返回2叉链b中data值为x的节点的层数。

#include #include "btree.h" int Level(BTNode *b,ElemType x,int h) { int l; if (b==NULL) return 0; else if (b->data==x) return h; else { l=Level(b->lchild,x,h+1); if (l==0) return Level(b->rchild,x,h+1); else return l; } } int main() { BTNode *b; CreateBTNode(b,"A(B(D,E(H(J,K(L,M(,N))))),C(F,G(,I)))"); printf("值为K的节点在2叉树中出现在第 %d 层上n",Level(b,K,1)); DestroyBTNode(b); return 0; }

（5）判断2叉树是不是类似（关于2叉树t1和t2类似的判断：①t1和t2都是空的2叉树，类似；②t1和t2之1为空，另外一不为空，则不类似；③t1的左子树和t2的左子树是类似的，且t1的右子树与t2的右子树是类似的，则t1和t2类似。）

#include #include "btree.h" int Like(BTNode *b1,BTNode *b2) { int like1,like2; if (b1==NULL && b2==NULL) return 1; else if (b1==NULL || b2==NULL) return 0; else { like1=Like(b1->lchild,b2->lchild); like2=Like(b1->rchild,b2->rchild); return (like1 & like2); } } int main() { BTNode *b1, *b2, *b3; CreateBTNode(b1,"B(D,E(H(J,K(L,M(,N)))))"); CreateBTNode(b2,"A(B(D(,G)),C(E,F))"); CreateBTNode(b3,"u(v(w(,x)),y(z,p))"); if(Like(b1, b2)) printf("b1和b2类似 "); else printf("b1和b2不类似 "); if(Like(b2, b3)) printf("b2和b3类似 "); else printf("b2和b3不类似 "); DestroyBTNode(b1); DestroyBTNode(b2); DestroyBTNode(b3); return 0; }

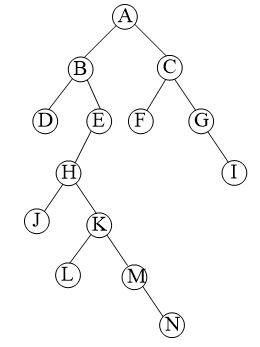
注：用”A(B(D,E(H(J,K(L,M(,N))))),C(F,G(,I)))”创建的用于测试的2叉树以下――

生活不易，码农辛苦
如果您觉得本网站对您的学习有所帮助,可以手机扫描二维码进行捐赠