您当前位置：首页 > php开源 > php教程 > 控制台绘制正弦/余弦曲线

控制台绘制正弦/余弦曲线

来源：程序员人生发布时间：2015-06-19 08:59:26 阅读次数：3403次

余弦曲线

固然了，这里我们不用数组……否则就没技术含量了。

正弦曲线的特点是左右对称，且左侧部份的纵坐标是从11直降到⑴的，相应的右侧的纵坐标是从⑴1直递增到1。难点在于显示器只能按行输出，也就是说输出了1行后不能再掉头输出上1行的信息。

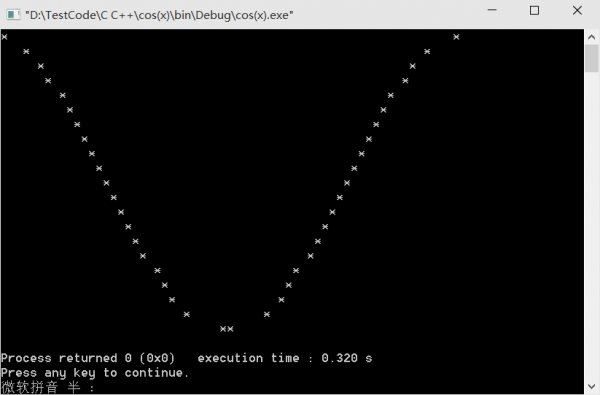
我们自定义1个缩放系数a为10，用acos(⑴)*10可以算得等于31，因此总宽度为62，出发点的横坐标为0，终点的横坐标为61。由于余弦曲线对称，所以在0~180度，也就是左侧部份时，横坐标为k时对应的相同纵坐标的180~360度，也就是右侧部份的横坐标为（62-k）。

#include <stdio.h>
#include <math.h>

int main()
{
    double y;
    int x,k;
    for(y=1;y>=-1;y-=0.1)
    {
        k=acos(y)*10;
        for(x=1;x<k;x++)
            printf(" ");
        printf("*");
        for(;x<62-k;x++)
            printf(" ");
        printf("*
");
    }
    return 0;
}

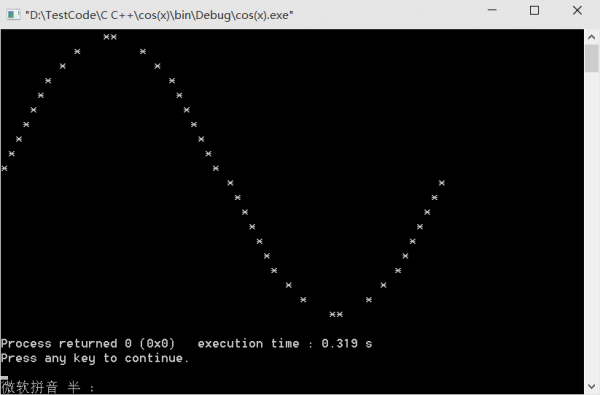
这里写图片描述

正弦曲线

正弦曲线就要难很多了……我们照旧沿用余弦曲线示例中的总宽度（62）。

相信对左侧部份大家都可以信手拈来……

        if(1<=k&&k<=15)
        {
            for(x=1;x<k;x++)
                printf(" ");
            printf("*");

            for(;x<30-k;x++)
                printf(" ");
            printf("*
");
        }

右侧部份我也弄了好久，主要是疏忽了asin(⑴)*10是负数……哎

所以发现了这1点以后就应当将if语句这样写：

if(-15<=k&&k<=-1)

但是还有1点要注意的，我们不是在用数组打印星号，换句话说，对横坐标而言，打印都得从1开始，而我们的坐标成了负值，该怎样办呢？

我们应当转换它：将负数k变成（31-k）它就成了1个公道的正数了，一样的，在270度的左右90之间也是对称的。而270度对应的宽度为46，那末180~270度之间的k对称到270~360度之间的多少呢？设1个方程就弄定了：

46-（31- k）= x - 46
=>
x = 61 + k

因而乎：

#include <stdio.h>
#include <math.h>

int main()
{
    double y;
    int x,k;
    for(y=1;y>=-1;y-=0.1)
    {
        k=asin(y)*10;

        if(1<=k&&k<=15)
        {
            for(x=1;x<k;x++)
                printf(" ");
            printf("*");

            for(;x<30-k;x++)
                printf(" ");
            printf("*
");
        }
        else if(-15<=k&&k<=-1)
        {
            for(x=1;x<31-k;x++)
                printf(" ");
            printf("*");

            for(x;x<61+k;x++)
                printf(" ");
            printf("*
");
        }
    }
    return 0;
}