您当前位置：首页 > php开源 > php教程 > 【codeforces #292(div 1)】ABC题解

【codeforces #292(div 1)】ABC题解

来源：程序员人生发布时间：2015-04-11 09:30:18 阅读次数：3242次

Drazil is playing a math game with Varda.

Let's define 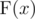$\text{[math]}$ for positive integer x as a product of factorials of its digits. For example, $\text{[math]}$ .

First, they choose a decimal number a consisting of n digits that contains at least one digit larger than 1. This number may possibly start with leading zeroes. Then they should find maximum positive number x satisfying following two conditions:

1. x doesn't contain neither digit 0 nor digit 1.

2. $\text{[math]}$ = $\text{[math]}$ .

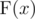Help friends find such number.

Input

The first line contains an integer n (1?≤?n?≤?15) ― the number of digits in a.

The second line contains n digits of a. There is at least one digit in a that is larger than 1. Number a may possibly contain leading zeroes.

Output

Output a maximum possible integer satisfying the conditions above. There should be no zeroes and ones in this number decimal representation.

Sample test(s)

input
4
1234

output
33222

input
3
555

output
555

Note

In the first case, $\text{[math]}$

贪心：

首先把原数x计算F(x)后所含有的123456789都统计出来。

然后把9拆成3*3；8拆成2*2*2；6拆成2*3；4拆成2*2；剩下的5和7不能拆，只能直接算阶乘。

最后就剩下了许多个3和许多个2了，此时31定比2少。

最后从大到小顺次输出7，5，3，2便可。

#include <iostream> #include <algorithm> #include <cstring> #include <cstdio> #include <cstdlib> using namespace std; char s[20]; int ans[10],cnt[10],a[10]; int main() { int n; scanf("%d",&n); scanf("%s",s); for (int i=0;i<n;i++) { int x=s[i]-'0'; for (int j=2;j<=x;j++) cnt[j]++; } a[1]=7,a[2]=5; for (int i=1;i<=2;i++) if (cnt[a[i]]) { ans[a[i]]=cnt[a[i]]; for (int j=2;j<=a[i];j++) cnt[j]-=ans[a[i]]; } cnt[3]+=(cnt[9]*2); cnt[2]+=(cnt[8]*3); cnt[2]+=cnt[6],cnt[3]+=cnt[6]; cnt[2]+=(cnt[4]*2); ans[3]=cnt[3],cnt[2]-=cnt[3]; ans[2]=cnt[2]; a[1]=7,a[2]=5,a[3]=3,a[4]=2; for (int i=1;i<=4;i++) for (int j=1;j<=ans[a[i]];j++) cout<<a[i]; cout<<endl; return 0; }

Drazil created a following problem about putting 1?×?2 tiles into an n?×?m grid:

"There is a grid with some cells that are empty and some cells that are occupied. You should use 1?×?2 tiles to cover all empty cells and no two tiles should cover each other. And you should print a solution about how to do it."

But Drazil doesn't like to write special checking program for this task. His friend, Varda advised him: "how about asking contestant only to print the solution when it exists and it is unique? Otherwise contestant may print 'Not unique' ".

Drazil found that the constraints for this task may be much larger than for the original task!

Can you solve this new problem?

Note that you should print 'Not unique' either when there exists no solution or when there exists several different solutions for the original task.

Input

The first line contains two integers n and m (1?≤?n,?m?≤?2000).

The following n lines describe the grid rows. Character '.' denotes an empty cell, and the character '*' denotes a cell that is occupied.

Output

If there is no solution or the solution is not unique, you should print the string "Not unique".

Otherwise you should print how to cover all empty cells with 1?×?2 tiles. Use characters "<>" to denote horizontal tiles and characters "^v" to denote vertical tiles. Refer to the sample test for the output format example.

Sample test(s)

input
3 3
...
.*.
...

output
Not unique

input
4 4
..**
*...
*.**
....

output
<>**
*^<>
*v**
<><>

input
2 4
*..*
....

output
*<>*
<><>

input
1 1
.

output
Not unique

input
1 1
*

output
*

Note

In the first case, there are indeed two solutions:

<>^ ^*v v<>

and

^<> v*^ <>v

so the answer is "Not unique".

第1眼看到这道题心想：这不是染色+2分图匹配吗？

然后就开始想怎样快速判断是不是2分图的完全匹配是不是唯1？？最后光荣的在第36个数据上T了。。（谁有快速的方法。。求告知vv）

看题解才知道，其实和2分图匹配1点关系都没有。。

有点类似于拓扑排序:能够用同1个纸片覆盖的格子连1条边，把两个格子的度数+1（两个格子之间最多1条边）。

扫描1次所有格子的度数，度数为1的加入队列，那末这些格子所对应的与他们1块被覆盖的格子是唯1的，出队以后把队列中对应格子的对应格子度数⑴，度数为1的再次入队。

如果队列为空以后，所有格子都被覆盖好了，那末此图有且唯一1个解；如果有格子没有被覆盖好，直接输出"Not unique"，可能无解，也可能多解（是哪一种就不用管了）

代码中Judge注释掉的部份是暴力用2分图来判定的；输出答案的部份直接用2分图来做了。

#include <iostream> #include <algorithm> #include <cstring> #include <cstdlib> #include <cstdio> #include <queue> using namespace std; int b,w,xx,yy,n,m,t,ti,v[2005][2005],fx[10][3],in[2005][2005],a[2005][2005],p[2005][2005]; char x[10],s[2005]; struct data { int x,y; }my[2005][2005]; queue<data> q; bool dfs(int x,int y) { for (int i=1;i<=4;i++) { int nx=x+fx[i][1],ny=y+fx[i][2]; if (nx<1||ny<1||nx>n||ny>m||a[nx][ny]!=1||v[nx][ny]==t) continue; v[nx][ny]=t; if (!my[nx][ny].x||dfs(my[nx][ny].x,my[nx][ny].y)) { my[nx][ny].x=x,my[nx][ny].y=y; return true; } } return false; } bool dfs2(int x,int y,int k) { for (int i=1;i<=4;i++) { int nx=x+fx[i][1],ny=y+fx[i][2]; if (nx==xx&&ny==yy&&!k) continue; if (nx<1||ny<1||nx>n||ny>m||a[nx][ny]!=1||v[nx][ny]==t) continue; v[nx][ny]=t; if (!my[nx][ny].x||dfs2(my[nx][ny].x,my[nx][ny].y,1)) { my[nx][ny].x=x,my[nx][ny].y=y; return true; } } return false; } bool Judge() { /* for (int i=1;i<=n;i++) for (int j=1;j<=m;j++) if (!a[i][j]) { t++; for (int k=1;k<=4;k++) { int nx=i+fx[k][1],ny=j+fx[k][2]; if (my[nx][ny].x==i&&my[nx][ny].y==j) xx=nx,yy=ny; } if (in[xx][yy]==1) continue; my[xx][yy].x=0; if (dfs2(i,j,0)) return false; my[xx][yy].x=i,my[xx][yy].y=j; } return true;*/ for (int i=1;i<=n;i++) for (int j=1;j<=m;j++) { v[i][j]=0; if (in[i][j]==1) { data x; x.x=i,x.y=j; q.push(x); } } while (!q.empty()) { data x=q.front(); q.pop(); if (v[x.x][x.y]) continue; v[x.x][x.y]=1; for (int i=1;i<=4;i++) { int nx=x.x+fx[i][1],ny=x.y+fx[i][2]; if (nx<1||ny<1||nx>n||ny>m||v[nx][ny]||a[nx][ny]==⑴) continue; v[nx][ny]=1; for (int j=1;j<=4;j++) { int nxx=nx+fx[j][1],nyy=ny+fx[j][2]; in[nxx][nyy]--; if (in[nxx][nyy]==1) { data X; X.x=nxx,X.y=nyy; q.push(X); } } } } for (int i=1;i<=n;i++) for (int j=1;j<=m;j++) if (a[i][j]!=⑴&&!v[i][j]) return false; return true; } void Print() { x[1]='*',x[2]='<',x[3]='>',x[4]='^',x[5]='v'; for (int i=1;i<=n;i++) for (int j=1;j<=m;j++) if (a[i][j]==1) { int x=my[i][j].x,y=my[i][j].y; if (x==i) { p[x][min(j,y)]=2,p[x][max(j,y)]=3; } else { p[min(x,i)][j]=4,p[max(x,i)][j]=5; } } for (int i=1;i<=n;i++) { for (int j=1;j<=m;j++) { if (!p[i][j]) printf("*"); else printf("%c",x[p[i][j]]); } printf(" "); } } int main() { fx[1][1]=fx[2][1]=0,fx[1][2]=1,fx[2][2]=⑴; fx[3][2]=fx[4][2]=0,fx[3][1]=1,fx[4][1]=⑴; scanf("%d%d",&n,&m); for (int i=1;i<=n;i++) { scanf("%s",s); for (int j=0;j<m;j++) { if (s[j]=='*') a[i][j+1]=⑴; else a[i][j+1]=1&(i+j+1); } } b=0,w=0; for (int i=1;i<=n;i++) for (int j=1;j<=m;j++) { if (a[i][j]==1) { b++; for (int k=1;k<=4;k++) { int nx=i+fx[k][1],ny=j+fx[k][2]; if (nx<1||ny<1||nx>n||ny>m) continue; if (a[nx][ny]==0)in[i][j]++,in[nx][ny]++; } } if (!a[i][j]) w++; } if (w!=b) { puts("Not unique"); return 0; } int ans=0; for (int i=1;i<=n;i++) for (int j=1;j<=m;j++) if (!a[i][j]) { t++; if (dfs(i,j)) ans++; } if (ans!=w) { puts("Not unique"); return 0; } if (Judge()) { Print(); } else { puts("Not unique"); } return 0; }

Drazil is a monkey. He lives in a circular park. There are n trees around the park. The distance between the i-th tree and (i?+?1)-st trees is di, the distance between the n-th tree and the first tree is dn. The height of the i-th tree is hi.

Drazil starts each day with the morning run. The morning run consists of the following steps:

Drazil chooses two different trees
He starts with climbing up the first tree
Then he climbs down the first tree, runs around the park (in one of two possible directions) to the second tree, and climbs on it
Then he finally climbs down the second tree.

But there are always children playing around some consecutive trees. Drazil can't stand children, so he can't choose the trees close to children. He even can't stay close to those trees.

If the two trees Drazil chooses are x-th and y-th, we can estimate the energy the morning run takes to him as 2(hx?+?hy)?+?dist(x,?y). Since there are children on exactly one of two arcs connecting x and y, the distance dist(x,?y) between trees x and yis uniquely defined.

Now, you know that on the i-th day children play between ai-th tree and bi-th tree. More formally, if ai?≤?bi, children play around the trees with indices from range [ai,?bi], otherwise they play around the trees with indices from 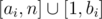$\text{[math]}$ .

Please help Drazil to determine which two trees he should choose in order to consume the most energy (since he wants to become fit and cool-looking monkey) and report the resulting amount of energy for each day.

Input

The first line contains two integer n and m (3?≤?n?≤?105, 1?≤?m?≤?105), denoting number of trees and number of days, respectively.

The second line contains n integers d1,?d2,?...,?dn (1?≤?di?≤?109), the distances between consecutive trees.

The third line contains n integers h1,?h2,?...,?hn (1?≤?hi?≤?109), the heights of trees.

Each of following m lines contains two integers ai and bi (1?≤?ai,?bi?≤?n) describing each new day. There are always at least two different trees Drazil can choose that are not affected by children.

Output

For each day print the answer in a separate line.

Sample test(s)

input
5 3
2 2 2 2 2
3 5 2 1 4
1 3
2 2
4 5

output
12
16
18

input
3 3
5 1 4
5 1 4
3 3
2 2
1 1

output
17
22
11

线段树/RMQ

首先复制1次，变环为链。

说说我的线段树做法：

对1个区间，保护3个值：

ma: “ |____|”的最大值

L_:“|__”的最大值

_R:“__|”的最大值

然落后行区间合并甚么的就能够了。

题解给出的是RMQ算法：

如果要求x-y这1段的值：(h[y]*2+d[1]+d[2]+d[3]+...d[y⑴])+(h[x]*2-d[1]-d[2]-d[3]-...-d[x⑴])

对第1部份记为A[y],第2部份记为B[x]，只要用RMQ求区间最大的A[]和B[]相加便可（可以证明顺序1定不会反过来）

我的线段树代码（1开始数组开到20w会RE...）

#include <iostream> #include <algorithm> #include <cstring> #include <cstdio> #include <cstdlib> #include <cmath> #define LL long long #define M 2000000+5 using namespace std; struct data { int l,r; LL ma,l_,_r; }a[M*2]; int n,m; LL h[M],s[M],d[M],inf; data Push_up(data a,data b) { data c; c.l=a.l,c.r=b.r; c.ma=max(a.l_+b._r+d[a.r],max(a.ma,b.ma)); c.l_=max(b.l_,a.l_+s[b.r⑴]-s[a.r⑴]); c._r=max(a._r,b._r+s[a.r]-s[a.l⑴]); return c; } void Build(int x,int l,int r) { a[x].l=l,a[x].r=r; if (l==r) { a[x].ma=-inf; a[x].l_=a[x]._r=h[l]; return; } int m=(l+r)>>1; Build(x<<1,l,m); Build((x<<1)+1,m+1,r); a[x]=Push_up(a[x<<1],a[(x<<1)+1]); } data Get(int x,int l,int r) { if (l<=a[x].l&&r>=a[x].r) return a[x]; int m=(a[x].l+a[x].r)>>1; if (r<=m) return Get(x<<1,l,r); if (l>m) return Get((x<<1)+1,l,r); return Push_up(Get(x<<1,l,r),Get((x<<1)+1,l,r)); } int main() { inf=(LL)1e18; scanf("%d%d",&n,&m); for (int i=1;i<=n;i++) cin>>d[i],d[n+i]=d[i]; for (int i=1;i<=n*2;i++) s[i]=s[i⑴]+d[i]; for (int i=1;i<=n;i++) cin>>h[i],h[i]*=2LL,h[n+i]=h[i]; Build(1,1,n*2); for (int i=1;i<=m;i++) { int l,r; scanf("%d%d",&l,&r); if (l<=r) cout<<Get(1,r+1,l⑴+n).ma<<endl; else cout<<Get(1,r+1,l⑴).ma<<endl; } return 0; }

感悟：

定式思惟太可怕。。。

生活不易，码农辛苦
如果您觉得本网站对您的学习有所帮助,可以手机扫描二维码进行捐赠
程序员人生

------分隔线----------------------------

上一篇 Spring发送邮件总结（附源码）

下一篇 Codeforces 520D. Cubes 贪心模拟

分享到:

------分隔线----------------------------

为码而活

积分：4237

15粉丝

7关注

栏目热点