复习机器学习算法：Logistic 回归

区分于线性回归，不是把每一个特点直接乘以系数，而是用1个S型函数（Logistic函数）。以下：

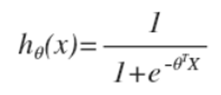
使用这类情势函数的缘由（几率、求导）。

代价函数，也不是线性回归中的误差平方和，而是基于对数似然函数，以下：

单个样本的后验几率为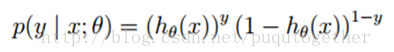：（y = 0， 1） 类似于2项散布的几率密度函数。

全部样本集的后验几率：

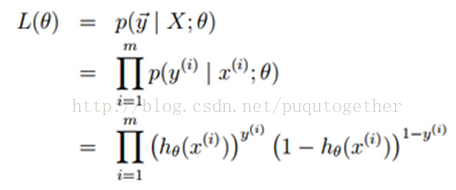
对数似然函数对代价函数，以下：

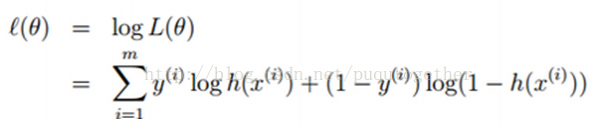
梯度降落法求解，对上面的代价函数求导，以下：

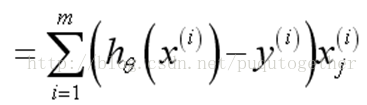
误差乘以对应的属性值，再求和。情势和线性回归1致，解释了为什么设计这样的S型函数和代价函数。这样的梯度降落法的计算量简单。

LR回归的优点：计算量小，从梯度降落法求导公式可以看出；可以处理非线性数据。

缺点：容易产生过拟合。

如何避免过拟合：

（1） 降维，可使用PCA算法把样本的维数下降，使得模型的theta的个数减少，次数也会下降，避免了过拟合；

（2） 正则化，设计正则项regularization term。

正则化作用就是避免某些属性前的系数权重过大，出现过拟合。

注意LR回归中解决过拟合的方式和决策树中解决的方法不同。

生活不易，码农辛苦
如果您觉得本网站对您的学习有所帮助,可以手机扫描二维码进行捐赠