算法系列笔记6(有关图的算法一―搜索,拓扑排序和强连通分支)
来源:程序员人生 发布时间:2015-03-13 07:56:54 阅读次数:3705次
简单概念:对图G(V,E),通常有两种存储的数据结构,1种是邻接矩阵,此时所需要的存储空间为O(V^2);第2种是邻接表,所需要的存储空间为O(V+E)。邻接表表示法存在很强的适应性,但是也有潜伏的不足,当要快速的肯定图中边(u,v)是不是存在,只能在顶点u的邻接表中搜索v,没有更快的方法,此时就能够使用邻接矩阵,但要以占用更多的存储空间作为代价;另外当图不是加权的,采取邻接矩阵存储还有1个优势:在存储邻接矩阵的每一个元素时,可以只用1个2进位,而没必要用1个字的空间。
图的搜索算法
搜索1个图示有序地沿着图的边访问所有的顶点,主要有两种搜索算法,广度优先遍历(bfs,也称为宽度遍历)和深度优先遍历(dfs)。
广度优先(bfs)
从源点s对图进行广度优先遍历,得到的路径为从源点s到其它各点的最短路径,也生成了1棵广度优先树。广度优先遍历需要1个队列,先进先出。
代码以下:
// 广度遍历图
void Graph::bfs(int s){
queue<int> q;
q.push(s);
visited[s] = 1;
while(!q.empty()){
int u = q.front();
q.pop();
cout << u <<" ";
GNode *p = edges[u].next;
while(p != NULL){
if(!visited[p->val]){ // 未被访问,则将其加入队列中并标志为访问过
q.push(p->val);
visited[p->val] = 1;
}
p = p->next;
}
}
}
void Graph::bfsTravel(){
memset(visited, 0, sizeof(int)*vertexNum);
for(int i = 0; i < vertexNum; i++){
if(!visited[i]){
bfs(i);
cout << endl;
}
}
}
时间复杂度为O(V+E)
深度优先(dfs)
深度优先搜素构成了1个由数棵深度优先树所组成的深度优先森林,每条边被称为树边。另外深度遍历对每一个节点会有个时间戳,用于标识该结点开始访问和结束访问的时间。1个重要的特性就是发现和完成时间具有括号结构。
代码以下:
// 深度优先遍历
void Graph::dfs(int s){
visited[s] = 1;
time += 1;
beginTime[s] = time;
cout << s << "(" << beginTime[s] << " "; // shen
GNode *p = edges[s].next;
while(p != NULL){
if(!visited[p->val])
dfs(p->val);
p = p->next;
}
time += 1;
endTime[s] = time;
topSort.push_back(s);
cout << endTime[s] << ")" <<" ";
}
void Graph::dfsTravel(){
memset(visited, 0, sizeof(int)*vertexNum);
memset(beginTime, 0, sizeof(int)*vertexNum); // 结点开始访问的时间
memset(endTime, 0, sizeof(int)*vertexNum); // 结点结束访问的时间
for(int i = 0; i < vertexNum; i++){
if(!visited[i]){
dfs(i);
cout << endl;
}
}
}
时间复杂度O(V+E)
注意:
对深度优先遍历,其边还可以划分为4类。
(1)树边,深度遍历森林中的每条边就是树边。
(2)前向边,u到其后裔的非树边(u,v)。
(3)反向边,u到其先人的边(u,v)。
(4)横向边,1个顶点就不是另外1个顶点的先人或后裔。
性质:(1)1个有向图是无回路的,当且仅当对该图的深度优先搜索没有产生反向边
(2)对1个无向图G进行深度优先搜索的进程中,G的每条边要末是树边,要末是反向边。
拓扑排序
有向无回路图(DAG,directed acyclic graph)的拓扑排序是深度优先搜索的1个利用。拓扑排序是对图G的所有顶点的1个线性序列,如果对图G中的边(u,v),则顶点u排在顶点v的前面。在很多利用中,有向无回路图用于说明事件产生的前后次序。
算法基本思想:通过对DAG图进行深度优先遍历以得到完成访问每一个结点的时间,其逆序就是DAG图的拓扑排序。
代码以下:已在深度遍历中体现。
时间复杂度为O(V+E)。
强连通分支
强连通分支为深度优先搜索的另外一个经典利用。有向图G=(V,E)的1个强连通分支就是1个最大顶点C是V的子集,使得C中任意两个顶点可以相互到达
图G的转置:GT=(V,ET),ET={(u,v):(u,v) ∈E}.由ET是由G的边改变方向后所组成的。建立GT所需要的时间复杂度也为O(V+E)
算法的基本思想:首先对图G进行深度优先搜索,据此得到图G的拓扑排序序列,然后将图GT依照此序列进行深度遍历,得到的括号结构便是所有的强连通分支。时间复杂度依然为O(V+E)
代码以下:
// 创建图g的转置
void Graph::buildTransGraph(Graph &g){
this->vertexNum = g.vertexNum;
this->edgesNum = g.edgesNum;
for(int i = 0; i < vertexNum; i++){
this->vertex[i] = g.vertex[i];
this->edges[i].val = g.edges[i].val;
this->edges[i].weight = g.edges[i].weight;
this->edges[i].next = NULL;
}
for(int i = 0; i < vertexNum; i++){
GNode *p = g.edges[i].next;
while(p != NULL){
GNode *newNode = new GNode();
newNode->val = i;
newNode->next = NULL;
newNode->weight = p->weight;
GNode *q = &edges[p->val];
while(q->next != NULL) q = q->next;
q->next = newNode;
p = p->next;
}
}
}
//强连通份量
void Graph::componentSC(){
//time = 0;
//dfsTravel(); // 对图g进行深度搜索得到完成x访问所需要的时间 并由此得到其拓扑排序
Graph g2;
g2.buildTransGraph(*this); // 得到图G的转置
time = 0;
memset(g2.visited, 0, sizeof(int)*vertexNum);
cout << "强连通份量: " << endl;
for(vector<int>::reverse_iterator iter = topSort.rbegin(); iter != topSort.rend(); iter++){ // 对转置图g2进行深度搜索得到强连通份量
if(!g2.visited[*iter])
g2.dfs(*iter);
}
cout << endl;
}
完全代码:
graph.h
#ifndef GRAPH_H
#define GRAPH_H
#include <iostream>
#include <vector>
using namespace std;
#define maxSize 10
#define maxInt 0x80000000 // 将此值设为权值的最大值
struct GNode{
int val;
int weight;
GNode *next;
};
class Graph{
public:
void createGraph(int n, int e);
void destroyGraph(GNode *p);
~Graph(){
for(int i = 0; i < vertexNum; i++){
destroyGraph(edges[i].next);
//cout << "析构:" << i << endl;
}
}
void showGraph();
void bfsTravel(); // 广度遍历
void dfsTravel(); // 深度遍历
void showTopSort(); // 输出拓扑序列
void componentSC(); // 建立图g的强连通份量
void prim();
private:
int vertex[maxSize]; // 寄存顶点
GNode edges[maxSize]; // 寄存邻接表
int vertexNum; //顶点个数
int edgesNum; //边条数
//bfs and dfs 遍历
int visited[maxSize];
void bfs(int s);
void dfs(int s);
int beginTime[maxSize]; // 深度开始访问x的时间
int endTime[maxSize]; // 结束访问x的时间
static int time;
vector<int> topSort; // topSort的逆序为有向无回路的拓扑排序
void buildTransGraph(Graph &g); // 建立图g的转置
// prim
int lowcost[maxSize];
};
#endif
graph.cpp
#include <iostream>
#include "graph.h"
#include <queue>
using namespace std;
int Graph::time = 0;
void Graph::createGraph(int n, int e){
vertexNum = n;
edgesNum = e;
for(int i = 0; i < n; i++){
vertex[i] = i;
edges[i].val = i;
edges[i].weight = 0;
edges[i].next = NULL;
}
for(int i = 0; i < e; i++){
int source, dest, wei;
cin >> source >> dest >> wei;
GNode *newNode = new GNode();
newNode->val = dest;
newNode->weight = wei;
newNode ->next = NULL;
GNode *p = &edges[source];
while(p->next != NULL) p = p->next;
p->next = newNode;
// 无向图 有向图就将这段删除掉
/*GNode *newNode2 = new GNode();
newNode2->val = source;
newNode2->weight = wei;
newNode2 ->next = NULL;
GNode *p2 = &edges[dest];
while(p2->next != NULL) p2 = p2->next;
p2->next = newNode2;*/
}
}
void Graph::destroyGraph(GNode *p){
if(p == NULL) return;
else{
destroyGraph(p->next);
delete p;
}
}
void Graph::showGraph(){
for(int i = 0; i < vertexNum; i++){
int j = i;
cout << i << "->";
GNode *p = edges[j].next;
while( p != NULL) {
cout << "(" << p->val <<"," << p->weight << ")" ;
p = p->next;
}
cout << endl;
}
}
// 广度遍历图
void Graph::bfs(int s){
queue<int> q;
q.push(s);
visited[s] = 1;
while(!q.empty()){
int u = q.front();
q.pop();
cout << u <<" ";
GNode *p = edges[u].next;
while(p != NULL){
if(!visited[p->val]){ // 未被访问,则将其加入队列中并标志为访问过
q.push(p->val);
visited[p->val] = 1;
}
p = p->next;
}
}
}
void Graph::bfsTravel(){
memset(visited, 0, sizeof(int)*vertexNum);
for(int i = 0; i < vertexNum; i++){
if(!visited[i]){
bfs(i);
cout << endl;
}
}
}
// 深度优先遍历
void Graph::dfs(int s){
visited[s] = 1;
time += 1;
beginTime[s] = time;
cout << s << "(" << beginTime[s] << " "; // shen
GNode *p = edges[s].next;
while(p != NULL){
if(!visited[p->val])
dfs(p->val);
p = p->next;
}
time += 1;
endTime[s] = time;
topSort.push_back(s);
cout << endTime[s] << ")" <<" ";
}
void Graph::dfsTravel(){
memset(visited, 0, sizeof(int)*vertexNum);
memset(beginTime, 0, sizeof(int)*vertexNum); // 结点开始访问的时间
memset(endTime, 0, sizeof(int)*vertexNum); // 结点结束访问的时间
for(int i = 0; i < vertexNum; i++){
if(!visited[i]){
dfs(i);
cout << endl;
}
}
}
// 输出拓扑排序
void Graph::showTopSort(){
for(vector<int>::reverse_iterator iter = topSort.rbegin(); iter != topSort.rend(); iter ++)
cout << *iter << " ";
cout << endl;
}
// 创建图g的转置
void Graph::buildTransGraph(Graph &g){
this->vertexNum = g.vertexNum;
this->edgesNum = g.edgesNum;
for(int i = 0; i < vertexNum; i++){
this->vertex[i] = g.vertex[i];
this->edges[i].val = g.edges[i].val;
this->edges[i].weight = g.edges[i].weight;
this->edges[i].next = NULL;
}
for(int i = 0; i < vertexNum; i++){
GNode *p = g.edges[i].next;
while(p != NULL){
GNode *newNode = new GNode();
newNode->val = i;
newNode->next = NULL;
newNode->weight = p->weight;
GNode *q = &edges[p->val];
while(q->next != NULL) q = q->next;
q->next = newNode;
p = p->next;
}
}
}
//强连通份量
void Graph::componentSC(){
//time = 0;
//dfsTravel(); // 对图g进行深度搜索得到完成x访问所需要的时间 并由此得到其拓扑排序
Graph g2;
g2.buildTransGraph(*this); // 得到图G的转置
time = 0;
memset(g2.visited, 0, sizeof(int)*vertexNum);
cout << "强连通份量: " << endl;
for(vector<int>::reverse_iterator iter = topSort.rbegin(); iter != topSort.rend(); iter++){ // 对转置图g2进行深度搜索得到强连通份量
if(!g2.visited[*iter])
g2.dfs(*iter);
}
cout << endl;
}
main.cpp
#include <iostream>
#include "graph.h"
using namespace std;
int main(){
Graph g;
g.createGraph(8, 13);
cout << "邻接表: " << endl;
g.showGraph();
cout << "广度遍历的结果: " << endl;
g.bfsTravel();
cout << "深度遍历的结果: " << endl; // 具有括号结果 其中x(a b) x代表结点 a代表开始访问x的时间 b代表完成访问x的时间
g.dfsTravel(); // 深度遍历完成访问x的时间的逆序就是有向无回路的拓扑排序
cout << "拓扑排序: " << endl;
g.showTopSort();
g.componentSC();
return 0;
}
图例:
待传...
输入:
0 1 1
1 2 1
2 0 1
1 3 1
3 4 1
4 3 1
2 5 1
5 6 1
6 5 1
3 6 1
6 7 1
7 7 1
4 7 1
输出:
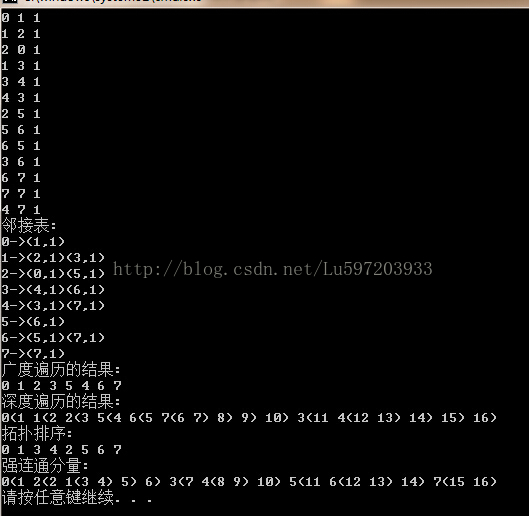
其中0(1 2(2 3) 4)表示在深度遍历中第0个结点开始访问结点的时间为1,结束访问结点的时间为4;2结点开始访问的时间为2,结束访问的时间为3.
生活不易,码农辛苦
如果您觉得本网站对您的学习有所帮助,可以手机扫描二维码进行捐赠


