数据结构基础(4) --快速排序
来源:程序员人生 发布时间:2015-01-07 08:58:38 阅读次数:2512次
快速排序是最流行的,也是速度最快的排序算法(C++ STL 的sort函数就是实现的快速排序); 快速排序(Quicksort)是对冒泡排序的1种改进。由C. A. R. Hoare在1962年提出。它的基本思想是:通过1趟排序将要排序的数据分割成独立的两部份,其中1部份的所有数据都比另外1部份的所有数据都要小,然后再按此方法对这两部份数据分别进行快速排序,全部排序进程可以递归进行,以此到达全部数据序列变成有序序列。其算法的特点就是有1个枢轴(pivot), 枢轴左侧的元素都小于/等于枢轴所指向的元素, 枢轴右侧的元素都大于枢轴指向的元素;
快速排序算法思想:
设要排序的数组是A[0], ..., A[N⑴],首先任意选取1个数据作为standard(通常选用数组的最后1个数)作为关键数据,然后将所有比它小的数都放到它前面,所有比它大的数都放到它后面(其实只要保证所有比他小的元素都在其前面,则后1条件则自动满足了),这个进程称为1趟快速排序。值得注意的是,快速排序不是1种稳定的排序算法,也就是说,多个相同的值的相对位置或许会在算法结束时产生变动。(信息来源:百度百科)
1次划分
目标:
找1个记录,以它的关键字/下标作为”枢轴/pivot”,凡是值小于枢轴的元素均移动至该枢轴所指向的记录之前,凡关键字大于枢轴的记录均移动至该记录以后。
导致1趟排序以后,记录的无序序列R[s..t]将分割成两部份:R[s..i⑴]和R[i+1..t],且
R[j].value ≤ R[i].value ≤ R[j].value
//实现
template <typename Type>
int partitionBy3Loop(Type *array, int p, int r)
{
int i = p;
int j = r+1; //j:超越末尾元素额下1位置
Type x = array[p]; //将最左侧的元素作为枢轴元素
//将<x的元素交换到左侧区域
//将>x的元素交换到右侧区域
while (true)
{
//找到1个比x大(>=x)的元素
while (i < r && array[++i] < x);
//找到1个比x小(<=x)的元素
while (array[--j] > x);
if (i >= j)
break;
//交换
std::swap(array[i], array[j]);
}
//将枢轴元素与array[p]进行交换
std::swap(array[p], array[j]);
//返回枢轴
return j;
}
/**说明:
几近国内所有的数据结构与算法的教材中的Partition实现都
类似于上面的那1种, 虽然易于理解,但实现过于复杂;
<算法导论>中给出了另外一种实现方式,
该方式虽然不容易于理解(其实明白其原理以后你就会爱上她),但是比较容易实现!
*/
template <typename Type>
int partitionBy1Loop(Type *array, int p, int r)
{
Type x = array[r]; //x作为终究枢轴所指向的元素
//i指向的是枢轴左侧的最后1个元素
//也就是与x左邻元素的下标
int i = p - 1;
//j则不断的寻觅下1个<=x的元素
for (int j = p; j < r; ++j)
{
if (array[j] <= x)
{
++ i;
std::swap(array[i], array[j]);
}
}
std::swap(array[i+1], array[r]);
//终究使得所有(i+1)左侧的元素都<=array[i+1],
//因此, 所有array[i+2:r]的元素都是大于array[i+1]的
return i+1;
}
快速排序
首先对无序的记录序列进行“1次划分”,以后分别对分割所得两个子序列“递归”进行快速排序。
//实现
template <typename Type>
void quickSort(Type *array, int p, int r)
{
if (p < r)
{
int pivot = partitionBy1Loop(array, p, r);
quickSort(array, p, pivot⑴);
quickSort(array, pivot+1, r);
}
}
快速排序的时间复杂性
假定1次划分所得枢轴位置 i = k,则对 n 个记录进行快排所需时间:
T(n) = {Tpass(n) + T(k⑴) + T(n-k) |Tpass(n)为对 n 个记录进行1次划分所需时间}
若待排序列中记录的关键字是随机散布的,则 k 取 1 至 n 中任意1值的可能性相同。
由此可得快速排序所需时间的平均值为:

设 Tavg(1)≤b,则可得结果:
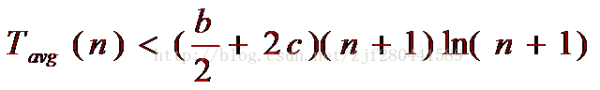
因此:快速排序的时间复杂度为O(nlogn)
若待排记录的初始状态为按关键字有序时,快速排序将堕落为起泡排序,其时间复杂度为O(n^2)。
为避免出现这类情况,需在进行1次划分之前,进行“预处理”,即:先对 R(s).key, R(t).key 和 R[?(s+t)/2?].key,进行相互比较,然后取关键字为3个元素中居中间的那个元素作为枢轴记录。
生活不易,码农辛苦
如果您觉得本网站对您的学习有所帮助,可以手机扫描二维码进行捐赠