《数据库系统概论》---第二章 关系数据库
来源:程序员人生 发布时间:2016-12-13 14:33:09 阅读次数:4610次
1、概述
1.关系模型的组成
数据结构:2维表(关系),数据库中全部数据和数据间的联系都以关系来表示。
数据操作:增、删、改、查
数据的束缚条件:实体完全性,参照完全性,用户自定义的完全性。
2.关系的数据结构
域
·是1组既有相同数据类的值的集合,又称值域。
·域中所包括值的个数称为域的基数。
笛卡尔积
·所有域的所有取值的1个组合;不能重复
·笛卡尔积的表示方法
笛卡尔积可表示为1个2维表
表中的每行对应1个元祖,表中的每个列对应1个域
关系
R(D1,D2,...Dn)
R:关系名 n:关系的目或度
表的每行对应1个元组,表的每列对应1个域。由于域可以相同,为了加以辨别,必须对每列起1个名字,称为属性。n目关系必有n个属性。
--元祖
关系中的元素是关系中的元祖,通经常使用t表示。
--关系的表示
关系也是1个2维表,表的每行对应1个组,表的每列对应1个域。
--属性
关系中不同的列可以对应相同的域
3.定义关系模式
R(U, D, DOM, F)
R 关系名
U 组成该关系的属性名集合
D 属性组U中属性所来自的域
DOM 属性向域的映像集
F 属性间的数据依赖关系
可简记为 R(U) 或 R(A1,A2,...,An)
A1,A2,...,An 属性名
关系模式
·关系模式是型,是稳定的
·关系是值 ,是动态的,随时间不断变化的
·关系模式是对关系的描写
3类关系
·基本关系
实际存在的表,是实际存储数据的逻辑表示
·查询表
查询结果对应的表
·视图表
由基本表或其他视图表导出的表,是虚表,不对应实际存储的数据。
基本关系的性质
·列是同质的
·不同的列可出自同1个域,其中每个列称为1个属性,不同的属性要给与不同的属性名
·列的顺序无所谓,列的次序可以交换
·任意两个元祖的候选码不能相同
·行的顺序无所谓,行的次序可以交换
·份量必须取原子值
4.基本关系操作
查询:选择、投影、选择、除、并、交、差
数据更新:插入、删除、修改
查询的表达能力是其中最重要的部份
选择、投影、并、差、笛卡尔积是5种最基本的操作
关系操作的特点
集合操作方式:操作的对象和结果都是集合,1次1集合的方式
2、关系的完全性
码
·候选码
若关系中的某1属性组的值能唯1地标识1个元组,则称该属性组为候选码。
简单的情况:候选码只包括1个属性
·全码
最极真个情况:关系模式的所有属性组是这个关系模式的候选码,称为全码
·主码
若1个关系有多个候选码,则选定其中的1个作为主码。每一个关系一定有且1个主码。
·外码
设F是基本关系R的1个或1组属性,但不是关系R的码。如果F与基本关系S的主码Ks相对应,则称F是基本关系R的外码。
(基本关系R称为参照关系;基本关系S称为被参照关系或目标关系)
3类完全性束缚
实体完全性、参照完全性、用户自定义完全性
1.实体完全性
实体完全性必须满足
a.主属性非空;b.主码各不相同
2.参照完全性
如果关系R2的外码F与R1的主码p相对应,则R2中的每个元祖在F上的取值:
a.或为空值;b.或等于R1中某个元组的p值
3.用户自定义的完全性
用户针对具体的利用环境定义的完全性束缚条件。
例如:“成绩”不能为负数,“性别”要求取值为“男”或“女”,“工龄”应当小于“年龄” 等。
3、关系代数
关系代数:将关系作为运算单位,用关系代数表达式表示的代数运算。
关系操作:传统的集合运算和专门的关系运算
1.传统的集合运算
除笛卡尔积外,要求参加运算的关系必须具有相容性。
定义:设给定两个关系R、S,若满足:
(1) 具有相同的度n,
(2) R中第i个属性和S中第i个属性来自同1个域,则说关系R、S是相容的。
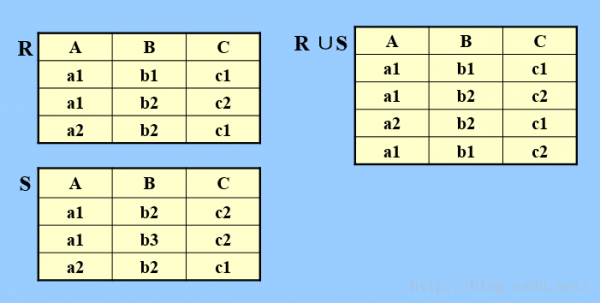
a.并
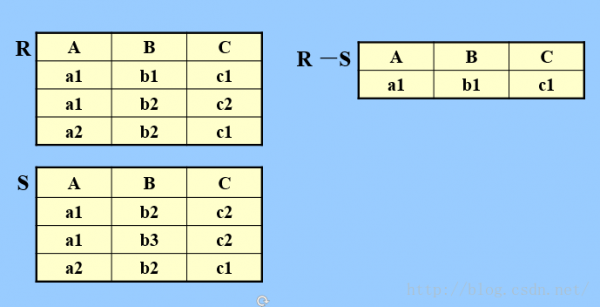
b.差
R和S具有相同的目n,相应的属性取自同1个域。
R-S :仍为n目关系,由属于R且不属于S的元组组成。
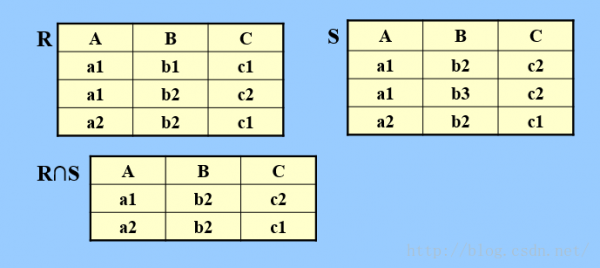
c.交
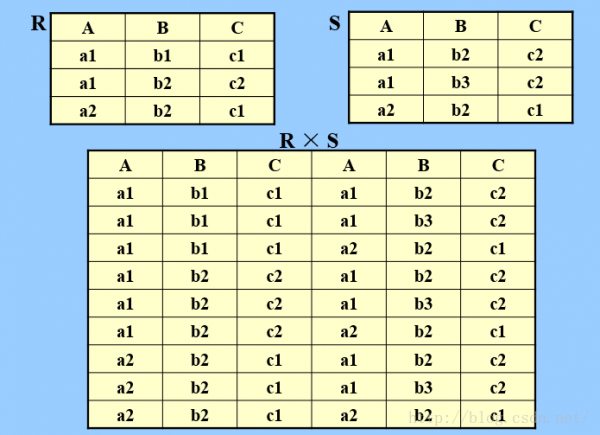
d.笛卡尔积 R X S
R:n目关系,k1个元组 S:m目关系,k2个元组
R X S:
列:(m+n)列元祖; 行:k1 X k2 个元组
2.专门的关系运算
a.选择;
选择操作是根据某些条件对关系做水平分割,即选取符合条件的元组构成结果关系。
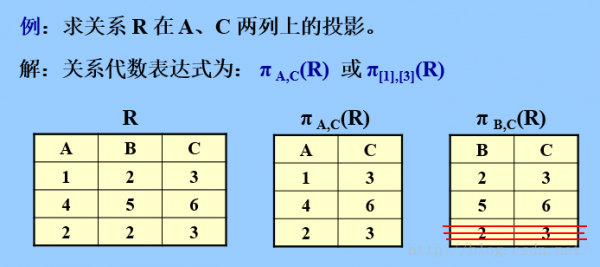
b.投影;
关系R上的投影是从R当选出若干属性列组成新的关系。
·特点:
1) 在单个关系上进行
2) 从列的角度进行运算
3) 投影的列可按自己的要求的顺序排列
·作用:
在关系当选择某些需要的列,并按要求组成1个新关系。
注意:投影后取消了某些属性列后,便可能出现重复行,应当删除这些完全相同的行。所以投影以后,不但属性减少了,元组也可能减少。
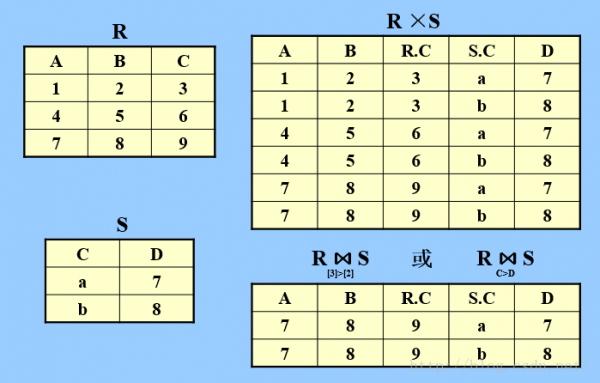
c.连接;
连接运算是从两个关系的笛卡尔积当选取满足连接条件的元组
记作:

其中A 和B 分别为 R 和 S 上度数相等且可比的属性组。θ是比较运算符(> ≥ = < ≤ ≠)。
运算步骤:
1) 求笛卡尔积 R×S
2) 选择其中满足AθB的元组
特点:
1) 两个关系参加运算,不1定有公共属性
2) θ为“=”时,称为等值连接
3) 结果关系中不去掉重复属性
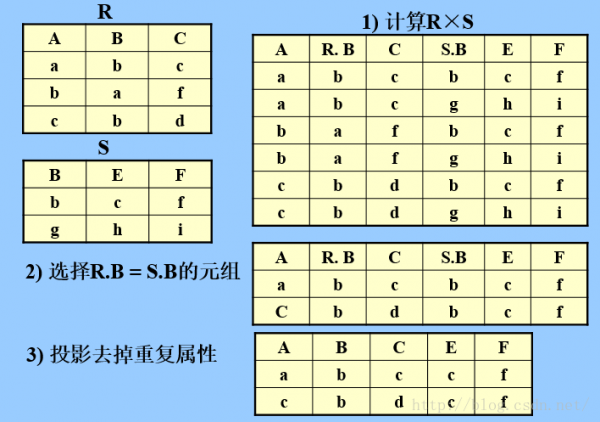
d.自然连接
自然连接与等值连接的区分:
自然连接中相等的份量必须是相同的属性组,并且要在结果中去掉重复的属性。
e.除法