关系代数运算

5种基本关系代数运算

集合：某些指定的对象集在1起就成了1个集合，其中每个对象叫元素。

集合的3特性：肯定性、互异性、无序性。

（1）肯定性：指的是概念清晰，对象描写明确，不能含糊不清、不能模棱两可。

（2）互异性：对1个给定的集合，它的任何两个元素都是不同的。

（3）无序性：给定的1个集合，集合内的元素间位置关系可以颠倒、调换。

5种基本关系运算：并、差、笛卡尔积、投影、选择。

我们学过集合的运算：并、交、差，求补集。

关系代数运算与集合的运算有相似的地方，且不完全相同。特别讲求位置关系，集合则是“无序性”。

1. 并（Union）：

关系代数并运算==集合并运算

关系R={a,b}，S={b,c}

R∪S = {a,b,c}.

2. 差（Difference）：

关系代数差运算==集合差运算

关系R和关系S，如果进行差运算，减数1定是被减数的子集。

关系R={a,b}，S={b}

R - S = {a}.

3. 笛卡尔积（Extended Cartesian Product）：

这是在之前的集合学习中没有的概念。

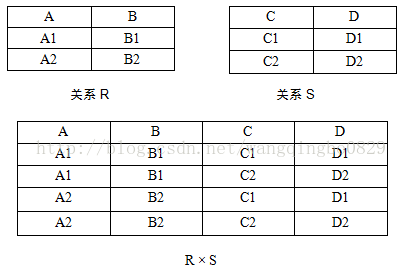
R × S 的元素个数等于关系R的元素个数与关系S的元素个数的乘积。

4. 投影（Projection）：

从垂直方向获得。

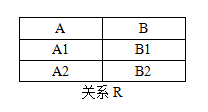
πA = {A1,A2}

5. 选择（Selection）：

从水平方向获得。

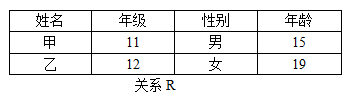
 σ年龄>16(R) = S 

总结：理论的介绍，目的在于传递1种思想，实现1种算法，所以进程必须尽量的简易。在实例中练习和加强。

援用文献：余运高  释疑集合的3大特性http://res.tongyi.com/resources/article/student/others/zt090318/zt/gz/sx/78.htm

生活不易，码农辛苦
如果您觉得本网站对您的学习有所帮助,可以手机扫描二维码进行捐赠