您当前位置：首页 > 互联网 > Codeforces Round #275 (Div. 2)

Codeforces Round #275 (Div. 2)

来源：程序员人生发布时间：2014-11-07 08:56:18 阅读次数：2194次

链接:http://codeforces.com/contest/483

Your friend has recently learned about coprime numbers. A pair of numbers {a,?b} is called coprime if the maximum number that divides both a and b is equal to one.

Your friend often comes up with different statements. He has recently supposed that if the pair (a,?b) is coprime and the pair (b,?c) is coprime, then the pair (a,?c) is coprime.

You want to find a counterexample for your friend's statement. Therefore, your task is to find three distinct numbers (a,?b,?c), for which the statement is false, and the numbers meet the condition l?≤?a?<?b?<?c?≤?r.

More specifically, you need to find three numbers (a,?b,?c), such that l?≤?a?<?b?<?c?≤?r, pairs (a,?b) and (b,?c) are coprime, and pair (a,?c) is not coprime.

Input

The single line contains two positive space-separated integers l, r (1?≤?l?≤?r?≤?10¹⁸; r?-?l?≤?50).

Output

Print three positive space-separated integers a, b, c ― three distinct numbers (a,?b,?c) that form the counterexample. If there are several solutions, you are allowed to print any of them. The numbers must be printed in ascending order.

If the counterexample does not exist, print the single number ⑴.

Sample test(s)

Input

2 4

Output

2 3 4

Input

10 11

Output

⑴

Input

900000000000000009 900000000000000029

Output

900000000000000009 900000000000000010 900000000000000021

Note

In the first sample pair (2,?4) is not coprime and pairs (2,?3) and (3,?4) are.

In the second sample you cannot form a group of three distinct integers, so the answer is ⑴.

In the third sample it is easy to see that numbers 900000000000000009 and 900000000000000021 are divisible by three.

简单构造：第1个数和第2个数互素，第2个数和第3个数互素，第1个数和第3个数不互素，明显找偶奇偶序列

#include <cstdio> #define ll long long ll gcd(ll a, ll b) { return b ? gcd(b, a % b) : a; } int main() { ll a, b; ll ans[3] = {0}; scanf("%I64d %I64d", &a, &b); if(b == a + 1) { printf("⑴ "); return 0; } if(a % 2 == 1) { ans[0] = a + 1; ans[1] = a + 2; } else { ans[0] = a; ans[1] = a + 1; } for(ll i = a + 2; i <= b; i++) { if(gcd(ans[1], i) == 1 && gcd(ans[0], i) != 1) { ans[2] = i; break; } } if(ans[2] == 0) { printf("⑴ "); return 0; } printf("%I64d %I64d %I64d ", ans[0], ans[1], ans[2]); }

You have two friends. You want to present each of them several positive integers. You want to present cnt₁ numbers to the first friend and cnt₂ numbers to the second friend. Moreover, you want all presented numbers to be distinct, that also means that no number should be presented to both friends.

In addition, the first friend does not like the numbers that are divisible without remainder by prime number x. The second one does not like the numbers that are divisible without remainder by prime number y. Of course, you're not going to present your friends numbers they don't like.

Your task is to find such minimum number v, that you can form presents using numbers from a set 1,?2,?...,?v. Of course you may choose not to present some numbers at all.

A positive integer number greater than 1 is called prime if it has no positive divisors other than 1 and itself.

Input

The only line contains four positive integers cnt₁, cnt₂, x, y (1?≤?cnt₁,?cnt₂?<?10⁹; cnt₁?+?cnt₂?≤?10⁹; 2?≤?x?<?y?≤?3・10⁴) ― the numbers that are described in the statement. It is guaranteed that numbers x, y are prime.

Output

Print a single integer ― the answer to the problem.

Sample test(s)

Input

3 1 2 3

Output

Input

1 3 2 3

Output

Note

In the first sample you give the set of numbers {1,?3,?5} to the first friend and the set of numbers {2} to the second friend. Note that if you give set {1,?3,?5} to the first friend, then we cannot give any of the numbers 1, 3, 5 to the second friend.

In the second sample you give the set of numbers {3} to the first friend, and the set of numbers {1,?2,?4} to the second friend. Thus, the answer to the problem is 4.

构造两个序列，第1个序列要有cnt1个数且其中不能有x的倍数，第2个序列要有cnt2个数且其中不能有y的倍数。要求求出这两个序列中的最大数的最小值。

如果答案是ans则ans＋1也满足可以发现问题满足2分做法的条件，cnt1个数为num - num / x，及1到num中不包括x倍数的数的个数，同理

cnt2个数为num - num / y，还有1点要注意的是必须满足cnt1 + cnt2 <= num - num / (x * y)由于题目要求两个集合中的元素不同，又由于x，y必定互素，所以cnt1和cnt2的和必须小于1到num中不包括(x * y)倍数的数的个数，不然两个集合必定出现重复元素，然后2分num的值即可以得到终究答案。

#include <cstdio> int cal(int a, int b) { return a - a / b; } int main() { int cnt1, cnt2, x, y; scanf("%d %d %d %d", &cnt1, &cnt2, &x, &y); int l = 1, r = 2e9; while(l < r) { int mid = l + (r - l) / 2; if(cnt1 <= cal(mid, x) && cnt2 <= cal(mid, y) && cnt1 + cnt2 <= cal(mid, x * y)) r = mid; else l = mid + 1; } printf("%d ", r); }

Permutation p is an ordered set of integers p₁,???p₂,???...,???p_n, consisting of n distinct positive integers not larger than n. We'll denote as n the length of permutation p₁,???p₂,???...,???p_n.

Your task is to find such permutation p of length n, that the group of numbers |p₁?-?p₂|,?|p₂?-?p₃|,?...,?|p_n?-?1?-?p_n| has exactly k distinct elements.

Input

The single line of the input contains two space-separated positive integers n, k (1?≤?k?<?n?≤?10⁵).

Output

Print n integers forming the permutation. If there are multiple answers, print any of them.

Sample test(s)

Input

3 2

Output

1 3 2

Input

3 1

Output

1 2 3

Input

5 2

Output

1 3 2 4 5

Note

By |x| we denote the absolute value of number x.

1个包括n个数的数列，要求相邻两元素差的绝对值的数的个数为k，要求构造这样的数列。

简单的构造题，k－－并变号判断便可

#include <cstdio> #include <cstring> int const MAX = 1e5 + 5; int a[MAX]; int hash[MAX]; int main() { int n, k; scanf("%d %d", &n, &k); memset(hash, 0, sizeof(hash)); a[1] = 1; hash[a[1]] = 1; int cnt = 1; for(int i = 2; i <= n; i++) { cnt++; a[i] = a[i - 1] + k; hash[a[i]] = 1; if(k > 0) k--; else k++; k *= ⑴; if(k == 0) break; } for(int i = 1; i <= n; i++) if(!hash[i]) a[++cnt] = i; for(int i = 1; i < n; i++) printf("%d ", a[i]); printf("%d ", a[n]); }

We'll call an array of n non-negative integers a[1],?a[2],?...,?a[n] interesting, if it meets m constraints. The i-th of the m constraints consists of three integers l_i, r_i, q_i (1?≤?l_i?≤?r_i?≤?n) meaning that value 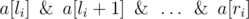$\text{[math]}$ should be equal to q_i.

Your task is to find any interesting array of n elements or state that such array doesn't exist.

Expression x&y means the bitwise AND of numbers x and y. In programming languages C++, Java and Python this operation is represented as "&", in Pascal ― as "and".

Input

The first line contains two integers n, m (1?≤?n?≤?10⁵, 1?≤?m?≤?10⁵) ― the number of elements in the array and the number of limits.

Each of the next m lines contains three integers l_i, r_i, q_i (1?≤?l_i?≤?r_i?≤?n, 0?≤?q_i?<?2³⁰) describing the i-th limit.

Output

If the interesting array exists, in the first line print "YES" (without the quotes) and in the second line print n integers a[1],?a[2],?...,?a[n] (0?≤?a[i]?<?2³⁰) decribing the interesting array. If there are multiple answers, print any of them.

If the interesting array doesn't exist, print "NO" (without the quotes) in the single line.

Sample test(s)

Input

3 1
1 3 3

Output

YES
3 3 3

Input

3 2
1 3 3
1 3 2

Output

NO

题意如题，还是构造数列，线段树保护＋判断

#include <cstdio> #include <cstring> #include <vector> using namespace std; int const MAX = 110000; struct Node { int l, r; int val; }; Node tree[10 * MAX]; Node a[MAX]; vector<int> ans; void build(int step, int l, int r) { tree[step].l = l; tree[step].r = r; tree[step].val = 0; if(l == r) return; int mid = (l + r) >> 1; build(step << 1, l, mid); build(((step << 1) + 1), mid+1, r); } void update(int step, int l, int r, int val) { if(tree[step].l == l && tree[step].r == r) { tree[step].val |= val; return; } int mid = (tree[step].l + tree[step].r) >> 1; if(r <= mid) update(step << 1, l, r, val); else if(l > mid) update((step << 1) + 1, l, r, val); else { update(step << 1, l, mid, val); update((step << 1) + 1, mid+1, r, val); } } int query(int step, int l, int r) { if(tree[step].l == l && tree[step].r == r) return tree[step].val; int mid = (tree[step].l + tree[step].r) >> 1; if(r <= mid) return query(step << 1, l, r); if(l > mid) return query((step << 1) + 1, l, r); else return query(step << 1, l, mid) & query((step << 1) + 1, mid+1, r); } void solve(int step) { if(step != 1) tree[step].val |= tree[step >> 1].val; if(tree[step].l == tree[step].r) { ans.push_back(tree[step].val); return ; } solve(step << 1); solve((step << 1) + 1); } int main() { int n, m; scanf("%d %d", &n, &m); build(1, 1, n); for(int i = 0; i < m; i++) { scanf("%d %d %d", &a[i].l, &a[i].r, &a[i].val); update(1, a[i].l, a[i].r, a[i].val); } bool flag = true; for(int i = 0; i < m; i++) { if(query(1, a[i].l, a[i].r) != a[i].val) { flag = false; break; } } solve(1); if(flag) { printf("YES "); for(int i = 0; i < ans.size(); i++) printf("%d%c",ans[i], i == n ? ' ' : ' '); ans.clear(); printf(" "); } else printf("NO "); }

生活不易，码农辛苦
如果您觉得本网站对您的学习有所帮助,可以手机扫描二维码进行捐赠
程序员人生

------分隔线----------------------------

上一篇 Bash Shell 解析路径获取文件名和目录名

下一篇 DNS查询工具使用浅析：host、nslookup、dig

分享到:

------分隔线----------------------------

为码而活

积分：4237

15粉丝

7关注

栏目热点