数据结构中树的基本定义相关概念汇总

定义

树的递归定义如下(个人比较喜欢的定义，源自百度百科)：

设T1,T2,..,Tk是树，它们的根结点分别为n1,n2,..,nk。用一个新结点n作为n1,n2,..,nk的父亲，则得到一棵新树，结点n就是新树的根。我们称n1,n2,..,nk为一组兄弟结点，它们都是结点n的子结点。我们还称T1,T2,..,Tk为结点n的子树。

空集合也是树，称为空树。空树中没有结点。

相关术语(源自维基百科,有改动)

1、节点的度：一个节点含有的子树的个数称为该节点的度；
2、树的度：一棵树中所有节点的度的最大值称为树的度；
3、叶节点或终端节点：度为零的节点；
4、非终端节点或分支节点：度不为零的节点；

5、父亲节点或父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点；
6、孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点；
7、兄弟节点：具有相同父节点的节点互称为兄弟节点；

8、节点的层次：定义一棵树的根节点层次为1，其他节点的层次是其父节点层次加1；
9、树的高度或深度：一棵树中所有节点的层次的最大值称为这棵树的深度；

10、堂兄弟节点：父节点在同一层的节点互为堂兄弟；
11、节点的祖先：从根到该节点所经分支上的所有节点；
12、子孙：以某节点为根的子树中任一节点都称为该节点的子孙。
13、森林：由m（m>=0）棵互不相交的树的集合称为森林；

需要说明下：节点＝结点，都源自英文单词node。叶节点＝叶子节点

种类

无序树：树中任意节点的子结点之间没有顺序关系，这种树称为无序树,也称为自由树;
有序树：树中任意节点的子结点之间有顺序关系，这种树称为有序树；

二叉树：每个节点最多含有两个子树的树称为二叉树；
二叉查找树（二叉排序树）
完全二叉树
满二叉树
平衡二叉树
霍夫曼树：带权路径最短的二叉树称为哈夫曼树或最优二叉树；

红黑树
B树

表示方法

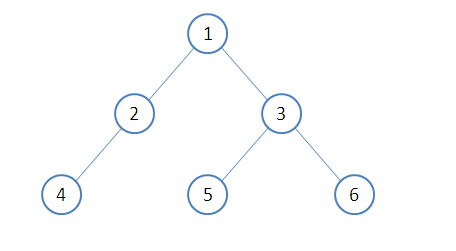
最直观的是树形表示法

还有另一个常用的方法：先将根结点放入一对圆括号中，根结点后紧跟一对圆括号，然后把它的子树按从左至右的顺序放入该括号中，同层子树之间用逗号隔开。如前文树形表示法可以表示为：（1（2（4），3（5，6）））

生活不易，码农辛苦
如果您觉得本网站对您的学习有所帮助,可以手机扫描二维码进行捐赠