UVA - 11927 Games Are Important (SG)

Description

Games Are Important

One of the primary hobbies (and research topics!) among Computing Science students at the University of Alberta is, of course, the playing of games. People here like playing games very much, but the problem is that the games may get solved completely--as happened in the case of Checkers. Generalization of games is the only hope, but worries that they will be solved linger still. Here is an example of a generalization of a two player game which can also be solved.

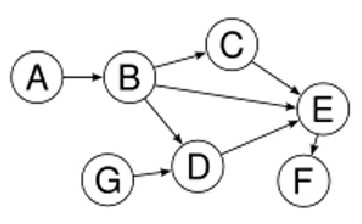
Suppose we have a directed acyclic graph with some number of stones at each node. Two players take turns moving a stone from any node to one of its neighbours, following a directed edge. The player that cannot move any stone loses the game. Note that multiple stones may occupy the same node at any given time.

Input 

The input consists of a number of test cases. Each test case begins with a line containing two integers n and m, the number of nodes and the number of edges respectively. ( 1n1000, 0m10000). Then, m lines follow, each containing two integers a and b: the starting and ending node of the edge (nodes are labeled from 0 to n - 1).

The test case is terminated by n more integers s₀,..., s_n-1 (one per line), where s_i represents the number of stones that are initially placed on node i ( 0si1000).

Each test case is followed by a blank line, and input is terminated by a line containing `0 0' which should not be processed.

Output 

For each test case output a single line with either the word ` First' if the first player will win, or the word ` Second' if the second player will win (assuming optimal play by both sides).

Sample Input 

4 3
0 1
1 2
2 3
1
0
0
0

7 7
0 1
0 2
0 4
2 3
4 5
5 6
4 3
1
0
1
0
1
0
0

0 0

Sample Output 

First
Second
有一个DAG(有向五环图)，每个结点上都有一些石子。两个玩家轮流把一个石头从一个结点沿着从此点出发的任意一条有向边移向相邻结点。不能移动的玩家算输掉游戏。注
意，在同一个时刻一个节点上可以有任意的石头。
思路：注意到，各个石头的状态的是完全独立的，所以这个游戏可以看做每个石头所形成的游戏的和。对于每一个石头，它的状态x就是所在的结点编号，如果此结点已经没有出发的边，则既是先手必败的状态，否则后续状态就是相邻结点的SG值集合。 
需要注意的是，对于在同一个结点来说，其上的石头如果个数为奇数，则当成1个石头即可；如果为偶数，可以忽略不计。这是由异或运算的性质决定的。 
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
const int maxn = 10005;

int n, m, sg[maxn];
vector<int> g[maxn];

int SG(int u) {
	if (sg[u] != -1)
		return sg[u];

	int vis[maxn];
	memset(vis, 0, sizeof(vis));
	for (int i = 0; i < g[u].size(); i++) {
		int tmp = SG(g[u][i]);
		vis[tmp] = 1;
	}

	for (int j = 0; ; j++)
		if (!vis[j]) {
			sg[u] = j;
			break;
		}
	return sg[u];
}

int main() {	
	int u, v;
	while (scanf("%d%d", &n, &m) != EOF && n+m) {
		memset(sg, -1, sizeof(sg));
		for (int i = 0; i < maxn; i++)
			g[i].clear();

		for (int i = 0; i < m; i++) {
			scanf("%d%d", &u, &v);
			g[u].push_back(v);
		}

		for (int i = 0; i < n; i++)
			sg[i] = SG(i);
	
		int ans = 0, u;
		for (int i = 0; i < n; i++) {
			scanf("%d", &u);
			if (u & 1)
				ans ^= sg[i];
		}
		printf("%s
", ans ? "First": "Second");
	}
	return 0;
}