用hadoop计算PI值

一、计算PI值的方式与原理

      百度一下，计算PI的方法还真不少。但在hadoop examples代码中的注释写的是：是采用 Quasi-Monte Carlo 算法来估算PI的值。 

      维基百科中对Quasi-Monte Carlo的描述比较理论，好多难懂的公式。 

      好在google了一把，找到了斯坦福大学网站上的一篇文章：《通过扔飞镖也能得出PI的值？》，文章很短，图文并茂，而且很好理解。 

      我这里将那篇文章的重要部分截了个图： 



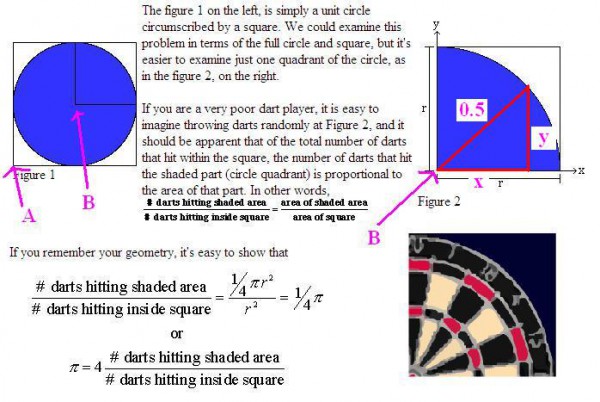
      对上面的图再稍微解释一下： 
      1、Figure2是Figure1的右上角的部分。 
      2、向Figure2中投掷飞镖若干次（一个很大的数目），并且每次都仍在不同的点上。 
      3、如果投掷的次数非常多，Figure2将被刺得“千疮百孔”。 
      4、这时，“投掷在圆里的次数”除以“总投掷次数”，再乘以4，就是PI的值！（具体的推导过程参见原文） 


      在这个算法中，很重要的一点是：如何做到“随机地向Figure2投掷”，就是说如何做到Figure2上的每个点被投中的概率相等。 

      hadoop examples代码中，使用了Halton sequence保证这一点，关于Halton sequence，大家可以参考维基百科。

      我这里再总结一下Halton sequence的作用： 在1乘1的正方形中，产生不重复，并且均匀的点。每个点的横坐标和纵坐标的值都在0和1之间。 

正是这样，保证了能够做到“随机地向Figure2投掷”。

      有人总结了一下，这个实际上叫做蒙特卡洛算法，我们取一个单位的正方形（1×1） 里面做一个内切圆（单位圆），则 单位正方形面积 ： 内切单位圆面积 = 单位正方形内的飞镖数 : 内切单位圆内的飞镖数 ，通过计算飞镖个数就可以把单位圆面积算出来， 通过面积，在把圆周率计算出来。 
注意 ，精度和你投掷的飞镖次数成正比。

二，运行hadoop估算PI的命令

     后面2个数字参数的含义： 
     第1个100指的是要运行100次map任务 
     第2个数字指的是每个map任务，要投掷多少次 

     2个参数的乘积就是总的投掷次数。 

     我运行的结果： 

三，总结

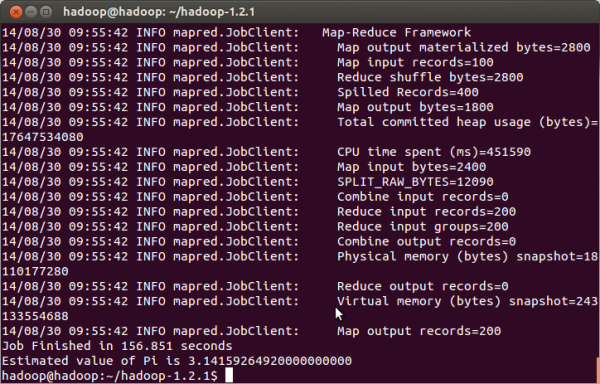
      hadoop的examples中的计算PI的方法属于是采用大量采样的统计学方法，还是属于数据密集型的工作。 

      转载请注明出处： http://www.ming-yue.cn/hadoop-pi/

生活不易，码农辛苦
如果您觉得本网站对您的学习有所帮助,可以手机扫描二维码进行捐赠